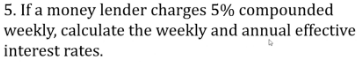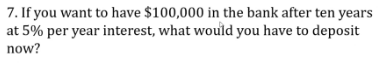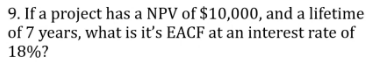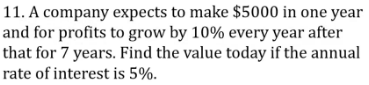Conference 5
Updated 2018-06-18
Conference 5
Agenda
- Midterm is take home: coming this weekend
- Any software or tool is allowed (open book)
- No collaboration
- Thesis is being looked at right now
Midterm Review
Engineering Costs
- Fixed costs/benefit: unchanging
- Variable costs/benefit: function of output
- Marginal costs/benefit: variable cost/benefit for one more unit
- Average costs/benefit: total divided by output
- Break-even point: level of output such that cost == revenue
- Sunk costs: :moneybag: spent and non-recoverable
- Opportunity costs: cost associated with resources being used for an alternative task
- Incremental cost: cost between alternatives
Cost Models
“Basically what generates these lines”:
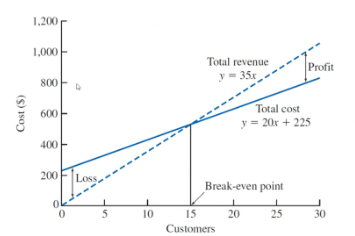
- Know how to make a model (cost and revenue)
- Understand the graph
- Understand the regions
Practice: break even
The marginal revenue is $8 per unit, so the break even point is 1000 units.
Cost Indexes
Know how to calculate cost given how it change historically as a ration relationship.
\[\frac{\text{Cost at }t_1}{\text{Cost at }t_2}=\frac{\text{Index value at }t_1}{\text{Index value at }t_2}\]Practice: cost indexes
Plug in into the cost index formula and we get $25518.35
Power Sizing Model
\[\frac{\text{Cost of A}}{\text{Cost of B}}=\left(\frac{\text{Size (capacity) of A}}{\text{Size (capacity) of B}}\right)^x\]Practice:
Learning Curve
Productivity increases over time/repetition.
\[T_N=T_0 \times N^b\\ \text{LC exponent}=\frac{\log(\text{LC percentage})}{\log2.0}, \qquad \text{LC percentage}=2^{\text{LC exponent}}\]Practice:
Cashflow Diagrams
- Know how to create a cashflow diagram
- They start at time 0 (now)
- Cashflow usually due at the end of the period (unless otherwise specified annuity due)
- Costs are negative, incomes are positive
Effective Interest Rate
- Know how to convert between nominal, yearly, and effective yearly rate.
- Effective monthly rate (\(i\)): \(i=\frac rm\)
- Effective yearly rate (\(i\)): \(i=(1+\frac rm)^m -1\)
Practice:
Answer: 5.12% annually and 0.0962% weekly.
Practice:
Answer: Nominal annual rate is \(1.5\%\times12\) compounded monthly. The effective annual interest rate is 19.6%.
Practice:
Answer: $61,391
Practice: uniform series
Answer: $20,742
Practice:
Answer: Use capital recovery factor
Practice:
Answer: Use single compound payment, 80.96 (which is \(i\))
Practice:
Answer: this is a geometric series $31,818
Practice:
Answer: note annuity due and we are looking for the annuity, so we divide by the term \((1+i)\); find \(A\) via \((A/P, n, i)\), which gives us
Practice:
Answer: perpetuity, $400 each year.
Practice:
Answer: $166,666 + $1M for the initial capital cost
Note: in certain cases, there might be overhaul, so we need to figure out the annuity for the future overhaul and convert that into the perpetual amount.
Practice:
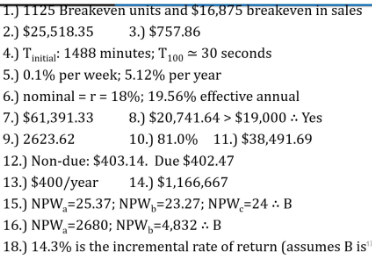
Answer: we need to make sure the analysis period is the same. Here it is convenient to use the LCM. Assumption is replacement placements for those that “die” out early.
For set A, we replace it at year 0, 3, 6, 9; set B at year 0, 4, 8, and set C just at year 0. The net worth for A, B, C is $, $, $24.
Alternative way is to calculate the EACF because they are repeatable purchases.
Practice:
Answer: B (higher NPW and higher internal rate of return (IRR))
Practice 17 does not exist
Practice:
Answer: calculate incremental rate of return; incremental IRR of 14.3%
Answer key:
Questions
Q: In ASN 2, should we buy the machine for 8 or the full 10 years?
You could buy for only 8 years and do something else for the last 2 years.
Q: Thesis outline example?
No, closest thing is the table of content from previous years.
Q: In ASN 2, is the 19% annual MARR nominal or effective?
Should be 19% nominal compounded annually. So monthly rate would be 19% divided by 12.
Q: For assignment 2 question 3 did we have to solve it monthly, or could we take yearly cashflows?
One can do it annually, but it’s tricky because there would be mid-period payments