Project 3 - Assignment

• 1. Transistor Size
  • Resistive-Load Inverter
  • Saturated-Enhancement-Load Inverter
  • Less-Saturated-Enhancement-Load Inverter
  • Comments
• 2. Buffer
  • DC Voltage Transfer Characteristics
  • Gain
  • CAD
• 3. Body Effect Factor
• 4. MOS Capacitances
  • Gate and Overlap Capacitances
  • Junction Capacitance
  • Drain Junction Capacitance
• 5. NOR Gate
  • Only Switching Input A
  • Tied Inputs A & B
  • Theory
  • Discrepancy
• 6. Inverter Noise Margin

1. Transistor Size

In the circuit of Figure below, design the widths of the pull-down transistors so that V_OL=0.1 V. (All transistors are minimum size, L = 0.1 μm. Explain the results.

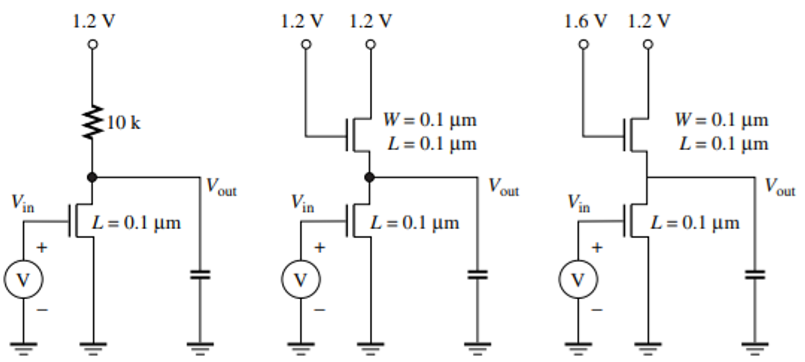
Since the diagrams don’t show how the transistor bulk are connected/biased, we can assume that there is no body-bias; and V_T = V_T0 = 0.4 V.

Resistive-Load Inverter

We first take a look at the extreme ends of operation. When Vin is high, VOH is VDD because the MOS is in cut-off. Thus no current flows through the resistor and the voltage drop across the resistor is 0.

Since our parameter of interest is V_OL and these are inverters, we are interested when the input voltage is HIGH.

The resistive load transistor operates in the linear region. So we equate the current in the resistor to the current through the NMOS (I_DS):

\[\frac{V_{DD}-V_{OL}}{R_L}=\frac{W}{L}\left(\frac{\mu_n C_{ox}}{1+\frac{V_{DS}}{E_c L}}\right)\left(V_{GS}-V_T-\frac{V_{DS}}{2}\right)V_{DS}\]

We substitute:

• V_GS is V_in which is also V_DD.
• V_DS is V_out which is also V_OL if the input voltage V_in is V_DD.
• V_DD is 1.2 V.
• V_OL is 0.1 V.
• R_L is 10 kΩ.
• L is 0.1 μm.
• μ_n is the mobility: 270 cm²V^-1s^-1.
• C_ox is the oxide capacitance: 1.6×10^-6 F/cm².
• E_C is the critical field: 6 V/μm.
• V_T is 0.4 V.

Isolate and solving for W:

\[W=\frac{L\times\frac{V_{DD}-V_{OL}}{R_L}}{\left(\frac{\mu_n C_{ox}}{1+\frac{V_{DS}}{E_c L}}\right)\left(V_{GS}-V_T-\frac{V_{DS}}{2}\right)V_{DS}}\]

Note that the centimeter (cm) cancels out when we multiply μ_n and C_ox. So we do the rest of the calculations with μm as the unit for length.

\[\begin{aligned} W&=\frac{0.1\times\frac{1.2-0.1}{10\times 10^3}}{\left(\frac{270\times 1.6\times 10^{-6}}{1+\frac{0.1}{(0.6)(0.1)}}\right)\left(1.2-0.4-\frac{0.1}{2}\right)0.1} \\ &=\frac{(0.1)(1.1\times10^{-4})}{(270\times1.6\times 10^{-6})(6/7)(0.075)} \\ &=0.396~\mathrm{\mu m} \end{aligned}\]

The width of the NMOS transistor for the resistive-load inverter is 0.4 μm.

Saturated-Enhancement-Load Inverter

Let’s denote the top transistor as L for load, and the bottom transistor as I for inverting. The top NMOS gate voltage is tied with V_DD, so it is always operating in saturation. The bottom transistor is still operating in linear mode.

Again, we start by equating the current of the top transistor with the bottom transistor: I_DSL = I _DSI.

\[\frac{W_I}{L_I}\cdot \frac{\mu_n C_{ox}}{1+\frac{V_{DS_I}}{E_C L_I}}\cdot\left(V_{GS_I}-V_T-\frac{V_{DS_I}}{2}\right)V_{DS_I} = W_L v_{sat}C_{ox}\cdot\frac{(V_{GS_L}-V_T)^2}{(V_{GS_L}-V_T)E_CL_L}\]

Where we substitute:

• V_GSI is just V_in.
• V_DSI is V_out.
• V_T is 0.4 V since we’re not assuming any body-bias effects.
• V_GSL is V_DD - V_out.

Isolate for W_I:

\[W_I=\frac{L_IW_L v_{sat}C_{ox}\cdot\frac{(V_{GS_L}-V_T)^2}{(V_{GS_L}-V_T)E_CL_L}}{\frac{\mu_n C_{ox}}{1+\frac{V_{DS_I}}{E_C L_I}}\cdot\left(V_{GS_I}-V_T-\frac{V_{DS_I}}{2}\right)V_{DS_I}}\times 10^{-4}\]

Also note that in order to use v_sat = 8×10⁶ cm/s, we need to convert this to μm/s, so we multiply the RHS of the equation by 1×10^-4.

\[W_I=\frac{(0.1)(0.1) (8\times 10^6)\cdot\frac{(1.2-0.1-0.4)^2}{(1.2-0.1-0.4)(6)(0.1)}}{\frac{(270) }{1+\frac{0.1}{(6)(0.1)}}\cdot\left(1.2-0.4-\frac{0.1}{2}\right)0.1}\times 10^{-4}\\ W_I=0.17~\mathrm{\mu m}\]

Less-Saturated-Enhancement-Load Inverter

In this case the gate voltage for the load transistor is 0.4 V higher than V_DD so the maximum output can be V_DD. But because the gate voltage is also higher, the top transistor is less-saturated.

Using the exact same equation as above, we use 1.6 - V_out instead for V_GSL. But V_in (for the bottom NMOS) remains at V_DD of 1.2 V.

\[W_I=\frac{(0.1)(0.1) (8\times 10 ^6)\cdot\frac{(1.6 - 0.1-0.4)^2}{(1.6 - 0.1-0.4)(6)(0.1)}}{\frac{270}{1+\frac{0.1}{(6)(0.1)}}\cdot\left(1.2-0.4-\frac{0.1}{2}\right)0.1}\times 10^{-4}\\ W_I=0.328~\mathrm{\mu m}\]

Comments

The resistive-load inverter is able to have a output voltage all the way up to V_DD which is good. But the resistor is cumbersome in digital design, and often means slower and bigger circuit. The size of the transistor thus is also relatively large at 0.4 μm.

Using the saturated-enhancement-load inverter, we no longer need the resistor. However, the maximum output voltage (high) is limited to V_DD - V_T. The trade-off is compensated with the small transistor size: at only 0.2 μm.

Lastly, we bias the gate voltage of the load NMOS exactly V_T higher to obtain a maximum high output voltage of V_DD. But the result is we use a substantially larger transistor: at 0.3 μm.

2. Buffer

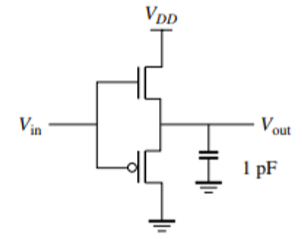
The design presented in the diagram is a buffer or voltage follower or something like the Redstone repeater from Minecraft.

Output swing: because the PMOS is the pull-down device, V_OL is at least V_TP, the threshold voltage from the PMOS. Similarly, because the NMOS is used as a pull-up device, V_OH is at most V_DD - V_TN.

DC Voltage Transfer Characteristics

• Starting from V_in of 0.0 V and slowly increasing it to V_T. The output won’t budget because the PMOS remains on while the NMOS remains off.
• After V_in = V_Tn + V_TP, the driving NMOS turns on and start to pull output up. The output voltage will keep increasing as we increase the input voltage, all the way to V_DD. By then, the output voltage is capped at V_DD - V_TN. V_DD - V_TP is where the PMOS fully turns off, which is close to where V_OH is.
• Now let’s go from input high to input low. The output won’t budge until V_in drops to V_DD - V_TP. because the pull-down PMOS is off.
• At V_in = V_DD - V_TP - V_TN and below, the PMOS gets stronger and pulls the output voltage back down to V_TP.

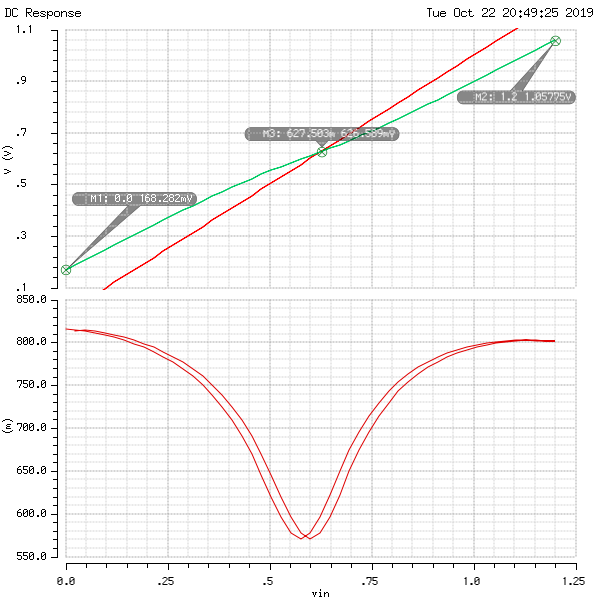
Notice that positive edge characteristics is different from negative edge, therefore we have hysteresis. It looks like this:

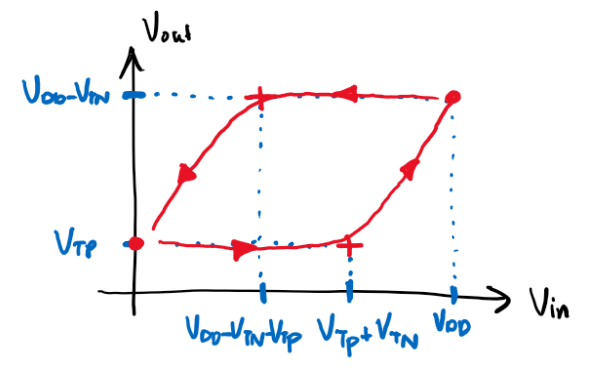
Gain

Theoretically, the gain should be close to 1 as output voltage follows input voltage. However, this is not a valid gate because it fails the following requirements:

• :x: High gain region is not between low gain regions.
• :x: Gain is higher than 1 for high gain region.
• :x: Low output is not below V_IL.
• :x: High output is not above V_IL.

In additional to lack of noise-rejection, this design also lack regenerative properties.

CAD

Below is the schematic. Since the bulk connection is not specified from the diagram. The bulk of the NMOS is connected to ground, and the bulk of the PMOS is connected to V_DD.

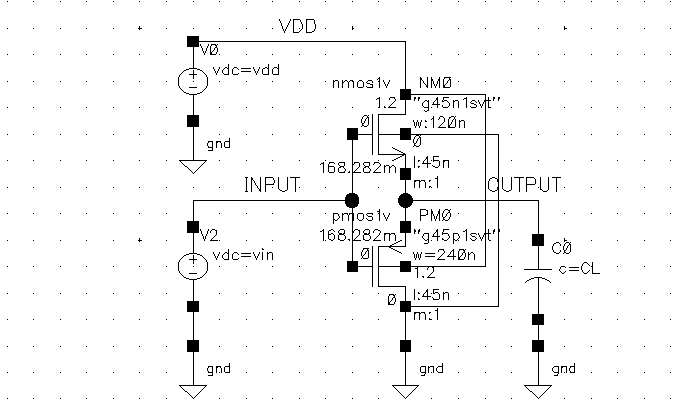
Running the DC sweep on V_in from 0V to 1.2V (V_DD) gets us the follow VTC plot. I also took the derivative of the green curve (VTC curve) so we can see that there exists hysteresis more clearly. The plot is a bit different from what I expected.

3. Body Effect Factor

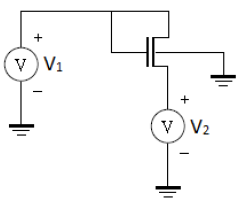
First model on CAD:

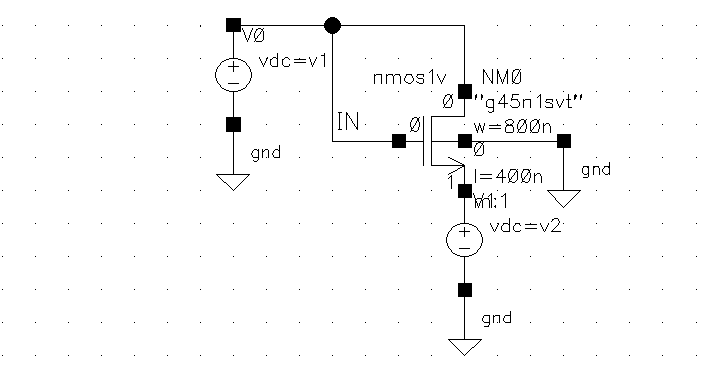
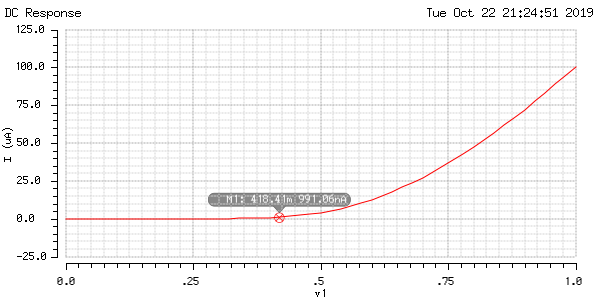
To take multiple samples, I fix V₂ to some value (0V, 0.2V, 0.4V, etc.). And then perform a DC sweep for V₁ from 0 V to 1.2 V. For each trial, V_T is where the current I_DS begin to rise: see below sample calculation and plot. I’m using 1 μA as a threshold to determine the V_T.

Here’s a table of data for V_T using different V₂ values:

V2 [V]	VT [V]
0.0	0.419
0.2	0.645
0.4	0.870
0.6	1.092
0.8	1.313

Using the data collected above, we can compute for the body-effect coefficient $\gamma$:

\[V_T = V_{T_0}+\gamma(\sqrt{V_{SB}+\vert2\phi_F\vert}-\sqrt{\vert2\phi_F\vert})\]

Where V_T0 is 0.4 V, V_SB is just V₂, and 2φ_F is 0.88V.

V_T0 is when the second term is zero. Since $\gamma$ and $2\phi_F$ is non-zero, the only case is when V_SB is 0. Which gives us V_T0=0.419 V.

I used Excel to compute the other data where V_SB=V₂ is not zero and using the formula:

\[\gamma=\frac{V_T-V_{T_0}}{\sqrt{V_{SB}+\vert 2\phi_F\vert}-\sqrt{\vert 2\phi_F\vert}}\]

V2 [V]	VT [V]	Body-Effect Coefficient [V½]
0.2	0.645	0.12
0.4	0.870	0.23
0.6	1.092	0.32
0.8	1.313	0.41

The body-efficient coefficient $\gamma$ varies with the voltage across source and bulk and it ranges between 0.12 and 0.41.

4. MOS Capacitances

Consider the layout in the figure below implemented in a 180nm technology. Assume that the transistor has W=900nm, L=180m, and a source/drain dimension Y=800nm and a lateral diffusion of 22nm. Let tox = 40 Å.

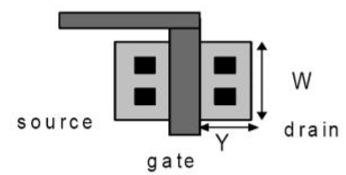
Gate and Overlap Capacitances

Compute the worst case gate capacitance per unit width, C_g in units of fF/μm. Estimate C_GS, C_GD and C_GB in linear, saturation, and cutoff, including overlap effects.

Let’s first find the oxide capacitance, which is a function of the thickness of the oxide layer.

\[C_{ox}=\frac{\epsilon_{ox}}{t_{ox}}\]

Where $\epsilon_{ox}$ is the silicon dioxide relative permissibility multiplied by the permissibility of free-space: $3.9\epsilon_0$. And the thickness $t_{ox}$ is 40 angstroms, or 40×10^-10 m.

Plugging in the values, we get values $C_{ox}=8.63$ F/μm².

Then the gate capacitance is simply multiplication by the length L:

\[C_g=C_{ox}L=(8.63)(0.18)=1.55~\mathrm{fF/\mu m}\]

Since the thickness of the gate, T_poly is not given, we assume that the fringe capacitance is negligible (C_f = 0).

The overlap capacitance for each overlap is given by the oxide capacitance multiplied by how much is overlapped (lateral diffusion L_D=22 nm).

\[C_{ol}=C_{ox}L_D=(8.63)(0.022)=0.19~\mathrm{fF/\mu m}\]

---

The total gate capacitance (which need us to multiply the numbers we got earlier with the width W) is

\[C_G=C_g W=(1.55)(0.9)=1.4~\mathrm{fF}\]

The total overlap capacitance for each overlap is

\[C_{OL}=C_{ol}W=(0.19)(0.9)=0.17~\mathrm{fF}\]

---

The capacitances broken down into the three parts: gate-source, gate-drain, and gate-bulk is as follows:

	Cutoff	[fF]	Saturation	[fF]	Linear	[fF]
VGS	COL	0.17	⅔CG+COL	1.10	½CG+COL	0.87
VGD	COL	0.17	COL	0.17	½CG+COL	0.87
VGB	CG	1.40	-	0.00	-	0.00

Junction Capacitance

First, we calculate the voltage asymptote: φ_B.

\[\begin{aligned} \phi_B&=\frac{kT}{q}\ln\left\vert\frac{N_AN_D}{n_i^2}\right\vert\\ &=2.565\times 10^{-2}\ln\left\vert\frac{(3\times 10^{16})(3\times 10^{19})}{(1.45\times 10^{10})^2}\right\vert\\ &=0.93~\text V \end{aligned}\]

Next, the zero-bias junction capacitance, where ε_si is the pure silicon permissibility at 11.7ε₀:

\[\begin{aligned} C_{j_0}&=\sqrt{\frac{\epsilon_{si} q}{2\phi_B}\cdot\frac{N_AN_B}{N_A+N_B}}\\ &=5.17\times10^{-8}~\text{F/cm}^2\\ &=0.517~\mathrm{fF/\mu m^2} \end{aligned}\]

Lastly, to get C_j, we multiply the per-area capacitance with the area: which is the bottom plate and the side walls.

\[\begin{aligned} C_j&=C_{j_0}(Y+2x_j)\\ &=C_{j_0}(0.8+2(0.3))\\ &=0.72~\mathrm{fF/\mu m} \end{aligned}\]

Drain Junction Capacitance

To calculate the junction capacitance, the formula is

\[C_J=\frac{C_{j}W}{\left(1-\frac{V_J}{\phi_B}\right)^m}\]

Where A is the area, V_J is the voltage across the junction, and m is ½.

When V_D is 1.8V the voltage across the junction is the voltage of the bulk subtract the drain voltage:

\[V_J = V_B-V_D=-1.8~\mathrm V\]

Plugging in, we get

\[C_J=\frac{(0.72)(0.9)}{\left(1-\frac{-1.8}{0.93}\right)}=0.222~\mathrm{fF}\]

When V_D is 0, the junction voltage is 0. So junction capacitance is simply

\[C_J=C_jW=(0.72)(0.9)=0.651~\mathrm{fF}\]

5. NOR Gate

Calculate Vs of 2-input NOR gates when one input is switching and with both inputs tied together. The device sizes are W_P = 24λ and W_N = 6λ. Use Cadence to find results when switching only input A, AB together. Results for two inputs switched separately vary slightly. Explain the discrepancy between theory and simulation.

First, I modelled the NOR gate in CAD. Note that I left the width property of the PMOS and NMOS as variable WP and WN. Here, we are using λ = 100nm.

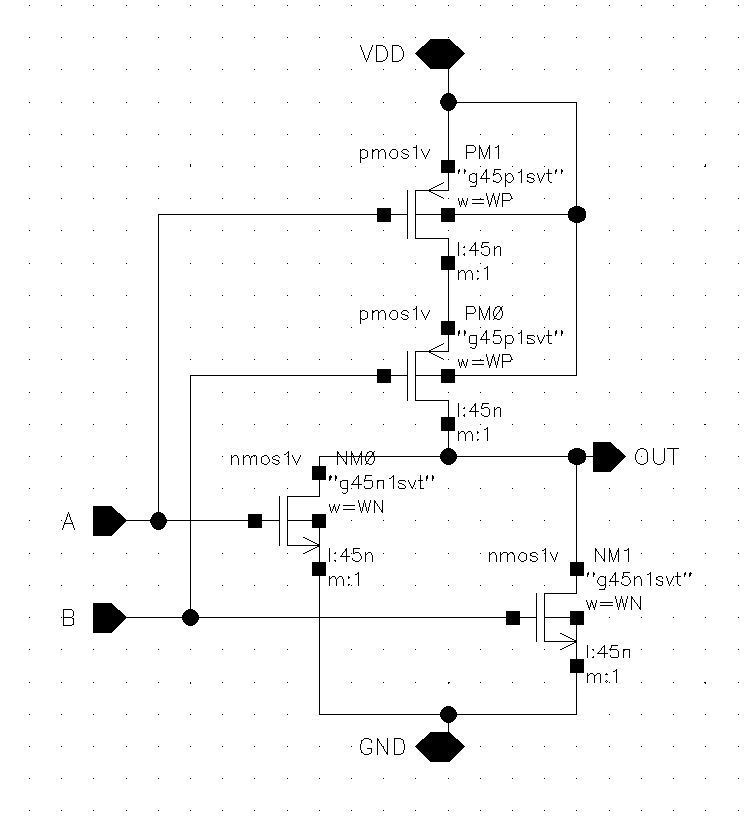
Only Switching Input A

Next, I created the test-bench for just switching input A:

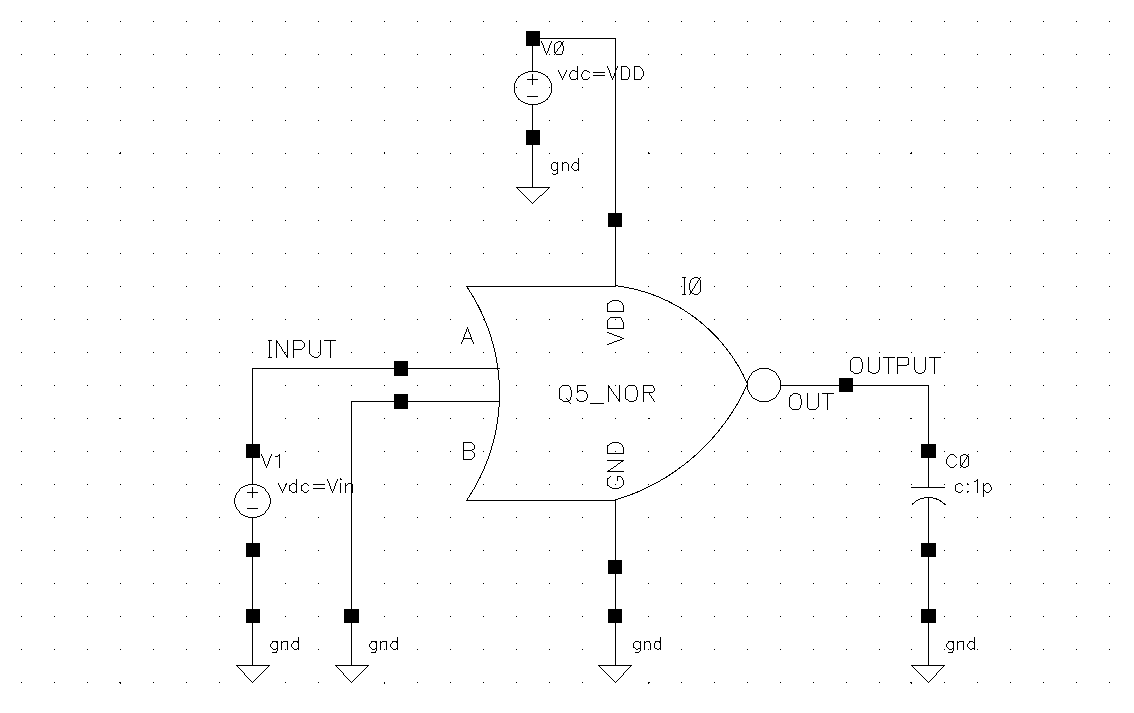
I setup the DC sweep analysis for Vin from 0V to 1.2V (V_DD). Here is the voltage transfer characteristics (VTC):

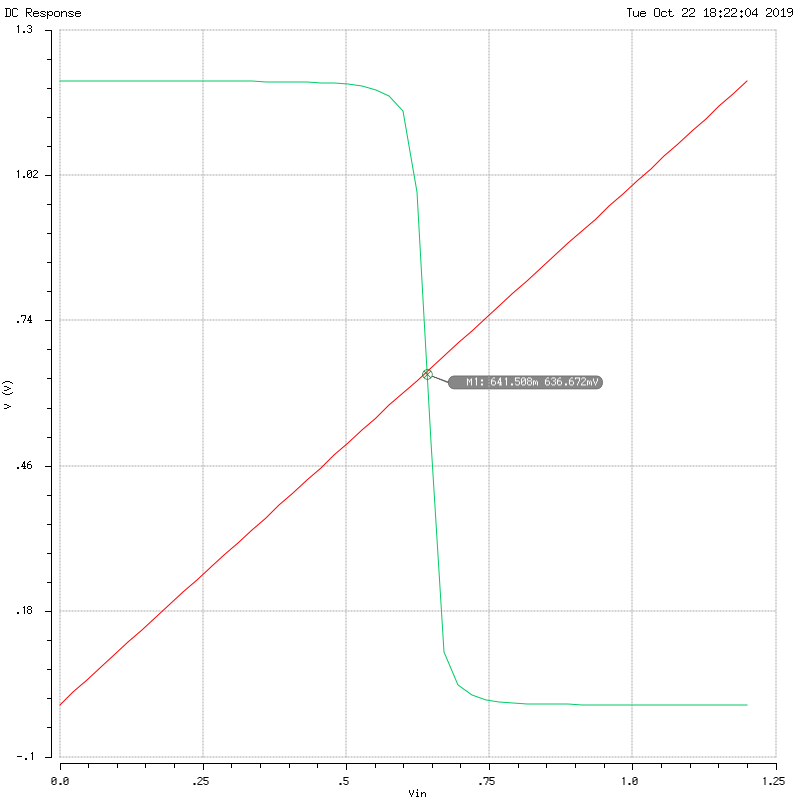
The switching voltage V_S = 0.642V.

Tied Inputs A & B

Now I modify the test-bench such that the input A and B are tied up together:

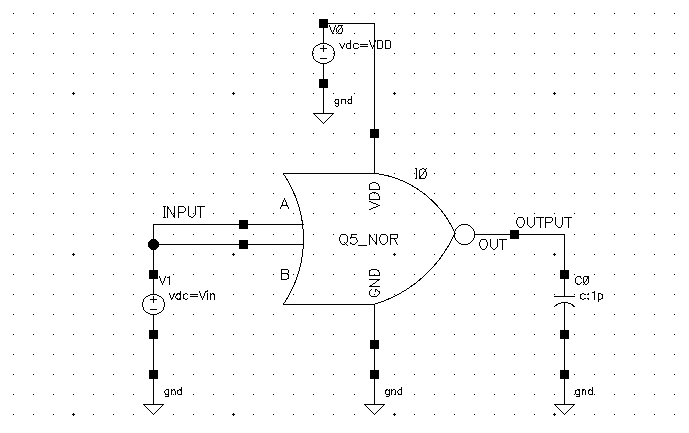
And here is the corresponding VTC plot:

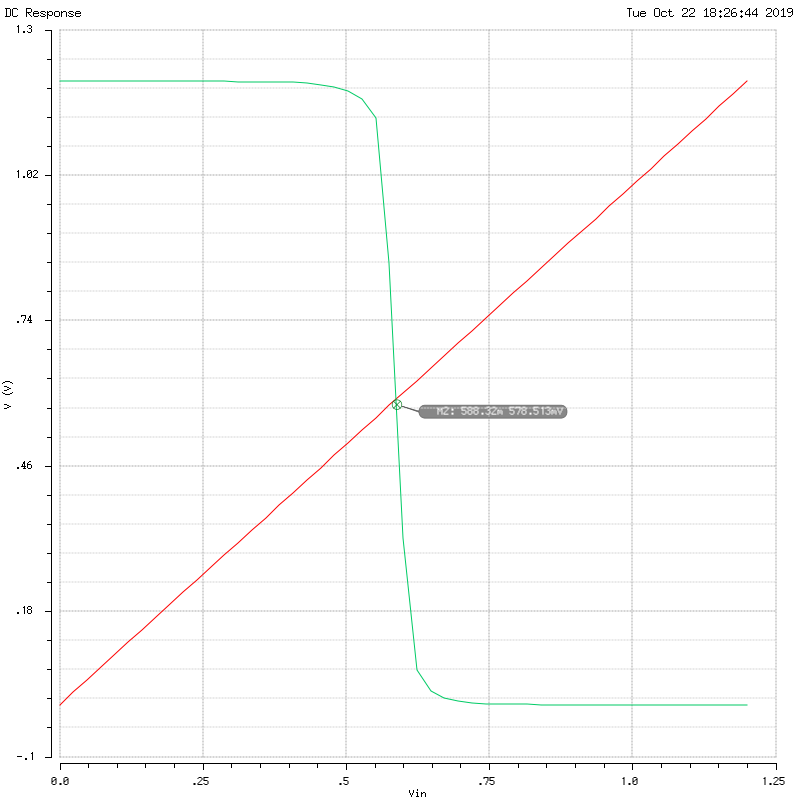
Now the switching voltage V_S = 0.588V has shifted to the left.

Theory

“How much stronger the NMOS is to the PMOS” can be described by the factor $\chi$:

\[\chi=\sqrt{\frac{W_N}{E_{CN}L_{N}}\frac{E_{CP}L_P}{W_P}}\]

And the switching voltage is given by:

\[V_s=\frac{V_{DD}-\vert V_{TP}\vert + \chi V_{TN}}{1+\chi}\]

So let’s find the threshold voltage first. Since the bulk of the PMOS are connected to V_DD and the bulk of the NMOS are connected to ground, V_SB = 0 for both, and therefore V_T is 0.4V.

The two extreme cases are: if only one input is switching, and if all inputs are tied as one. Any behavior of the gate (in terms of the VTC) is bracketed between these two cases.

Case 1: only A is switching:

As per standard CMOS design, for a NOR gate, the PMOS would be 4 times larger than the NMOS. However, because the MOS connected to B never switches and is grounded — the B-PMOS is a short, and B-NMOS is an open circuit.

The resulting (simplified) circuit is a single-input inverter:

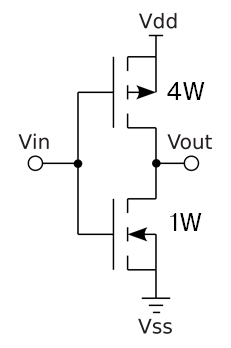
Note that in the diagram, I used “W” to show relative size of the NMOS and PMOS. To fit the problem description, W is equivalent to 6λ.

Compared to a standard inverter where the PMOS is suppose to have the double the width that of NMOS, we have 4 times the width. Meaning that the pull-up PMOS is much “stronger”. In other words, $\chi$ is smaller. Thus, we expect the VTC to shift to the right →.

Switching voltage:

\[\chi=\sqrt{\frac{W}{6}\frac{24}{4W}}=1\\ V_s=\frac{(1.2)-\vert -0.4\vert + (1)(0.4)}{1+1}=\frac{1.2}{2}=0.6~\text V\]

Case 2: all inputs tied:

Shorting all the inputs together and using the same simplification used for case 1, we get the following equivalent single-input inverter (adding resistances: 4W and 4W in series makes 2W; W and W in parallel makes 2W):

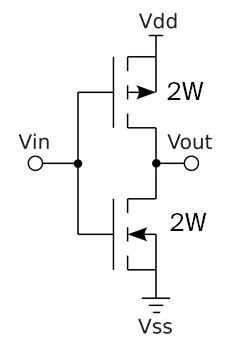
Now compared to the standard inverter, NMOS is now much stronger than PMOS (since it should’ve been half the size). So $\chi$ is larger, and we expect the VTC to shift to the left.

Switching voltage:

\[\chi=\sqrt{\frac{2W}{6}\frac{24}{2W}}=\sqrt{4}=2\\ V_s=\frac{(1.2)-\vert -0.4\vert + (2)(0.4)}{1+2}=\frac{1.6}{3}=0.53~\text V\]

Discrepancy

The calculated switching voltages are smaller compared to the voltage measured from the simulation. I suspect it’s because there exists unaccounted body-effect. This could change the threshold voltage V_T and thus change the switching voltage V_s. V_T of 0.56 V would gives us closer number to the one obtained from simulation.

6. Inverter Noise Margin

Using the following schematic and Cadence simulations find NM_H and NM_L.

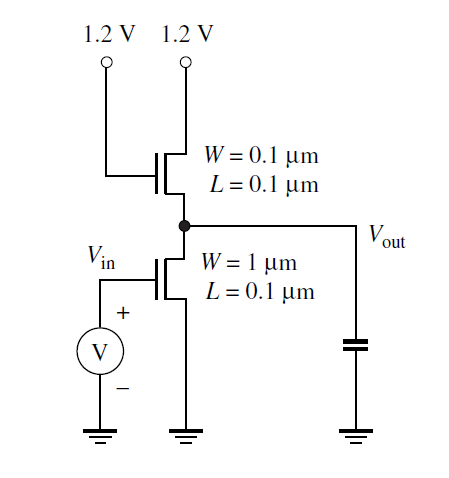
Note: for this problem, because the CAD library doesn’t allow sizes less than 120nm, we will use L=100nm for both NMOS, W=120nm for top NMOS, and W=1 μm for bottom NMOS.

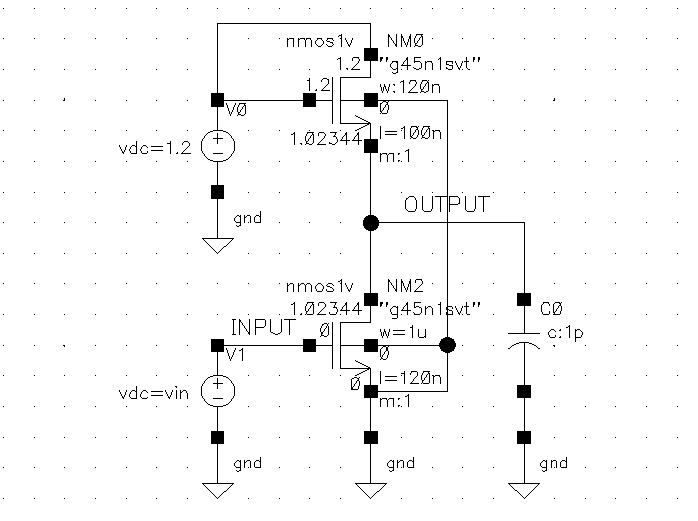
Here is the schematic of the the saturated-enhanced inverter cell view:

Here is the VTC plot of this circuit, DC sweeping the signal INPUT from 0.0V to V_DD (1.2V). The green curve is the OUTPUT signal.

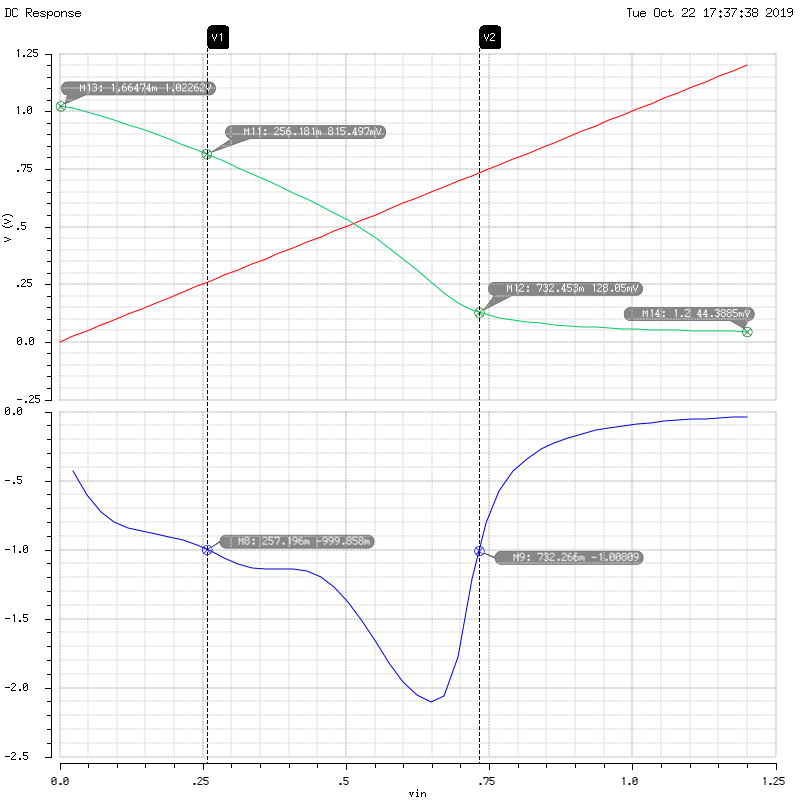
To find the noise margin, we must first find V_IL, and V_HH which corresponds to the positions on the green curve where the slope is -1. We can find the slope by taking the derivative of the graph (in blue).

Where the slope equals to -1 is where input voltage is 0.257V and 0.733V for low and high, respectively. Thus, V_IL = 0.257V and V_IH = 0.732V.

Next, by inspecting from the graph, the output low and high voltage are: V_OL = 0.044V and V_OH = 1.023V.

Finally, we have all the values to compute the noise margin:

\[NM_L=V_{IL}-V_{OL}=0.257-0.044=0.213~\text V\\ NM_H=V_{OH}-V_{IH}=1.023-0.732=0.290~\text V\]