Week 4 - Poles and Zeroes

Poles corresponds to the polynomial in the denominator of a transfer function in s-domain. Zeroes corresponds to the polynomial in the numerator. Consider the following examples:

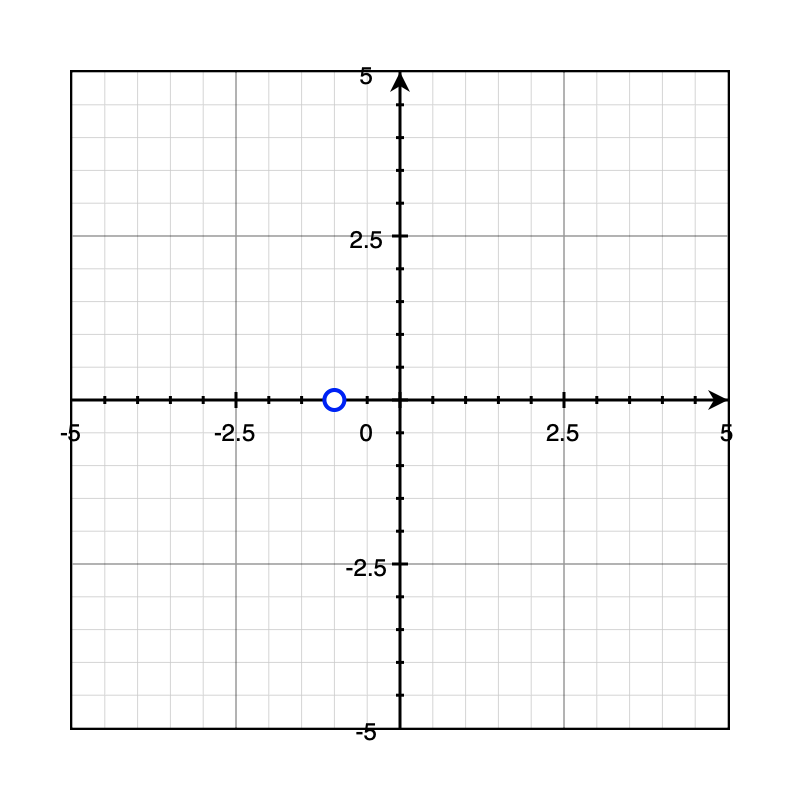
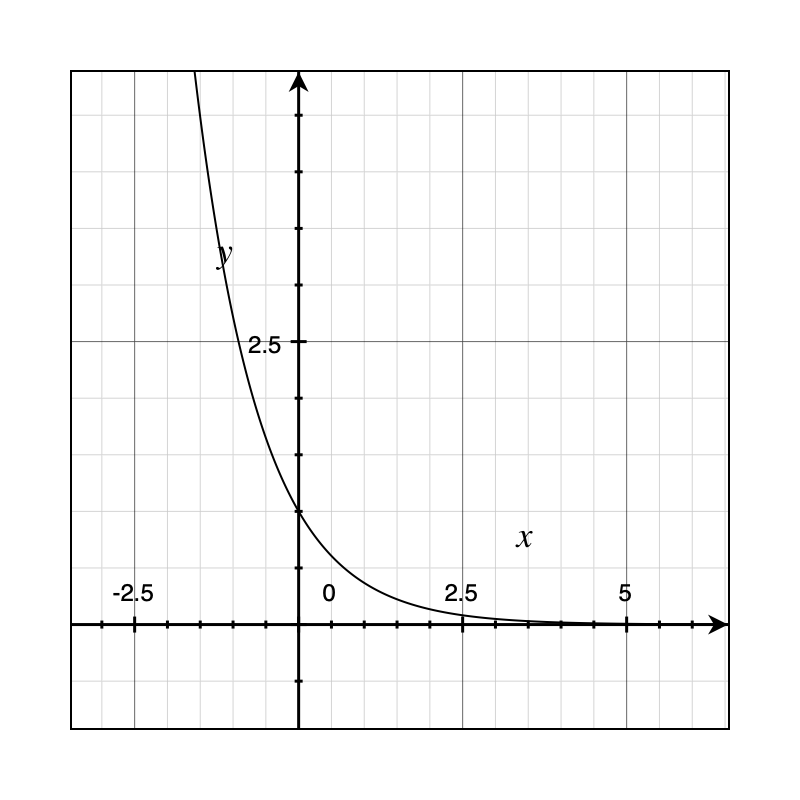
Example 1: Single pole on the left \(\frac{1}{s+1}\Rarr e^{-t}\)

This open loop transfer function has a pole on the left-hand side of the s-space. When plotted in time-domain, we see that this system is naturally stable.

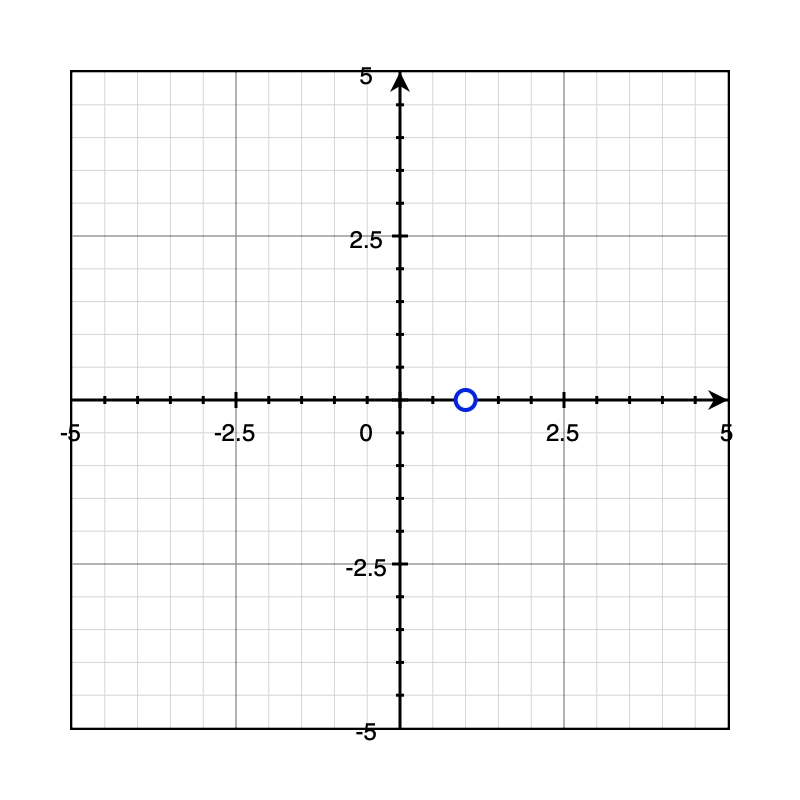
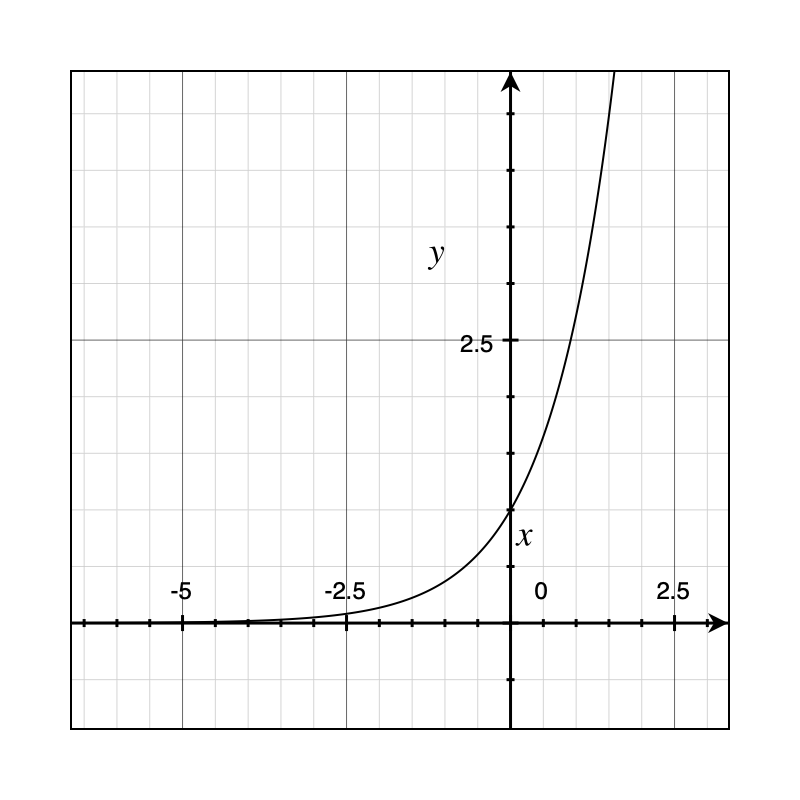
Example 2: Single pole on the right \(\frac{1}{s-1}\Rarr e^t\) The open loop transfer function has a pole on the right-hand side of the s-space. This is considered bad because it results in an unstable sytem. In time-domain, it is apparent that the signal will exponentially grow until saturation.

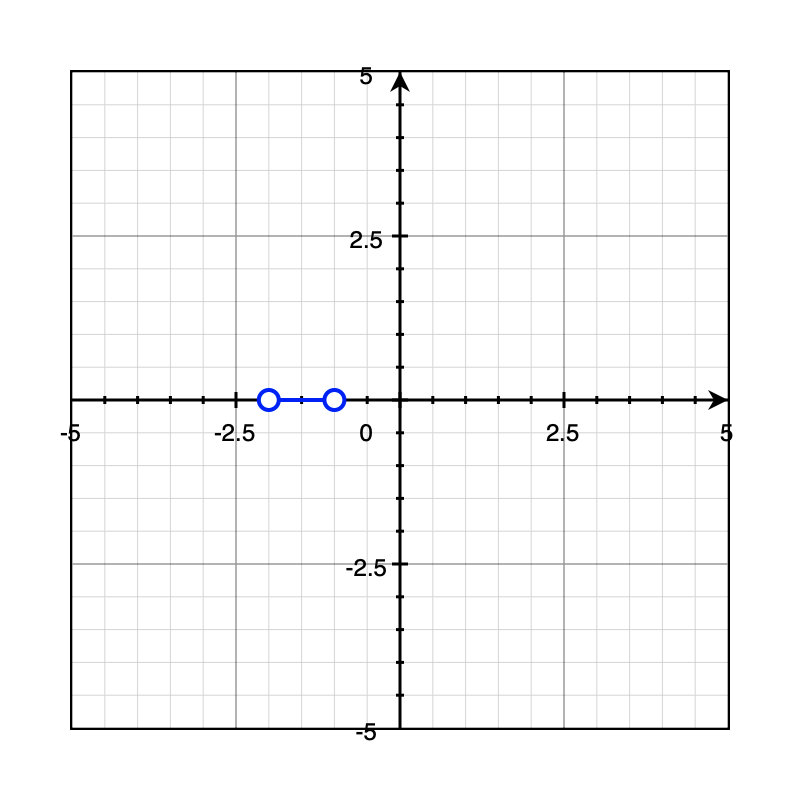
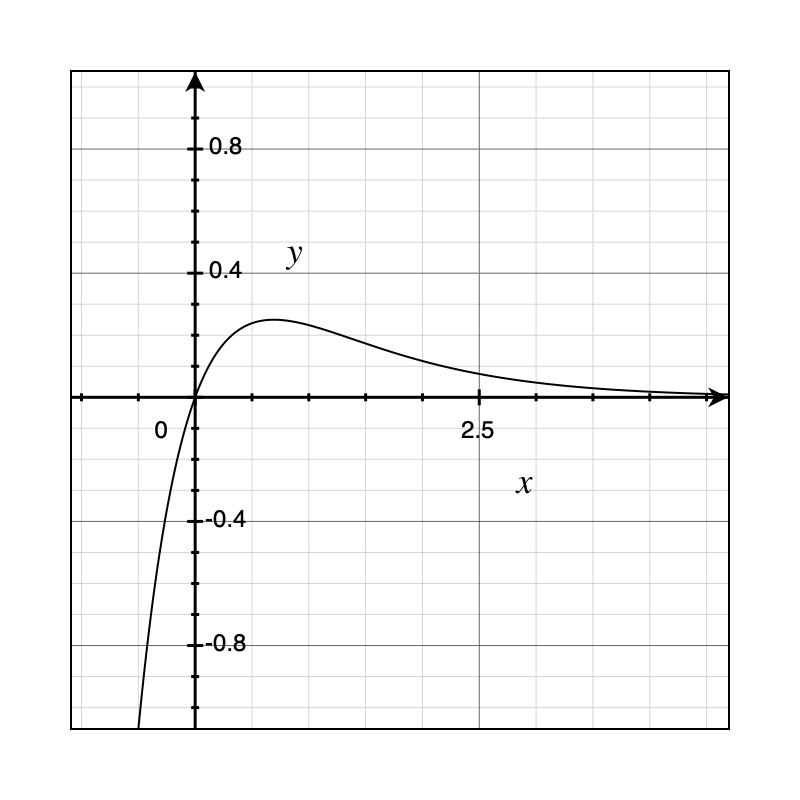
Example 3: Two poles on the left \(\frac{1}{(s+2)(s+1)}\Rarr e^{-t}-e^{-2t}\)

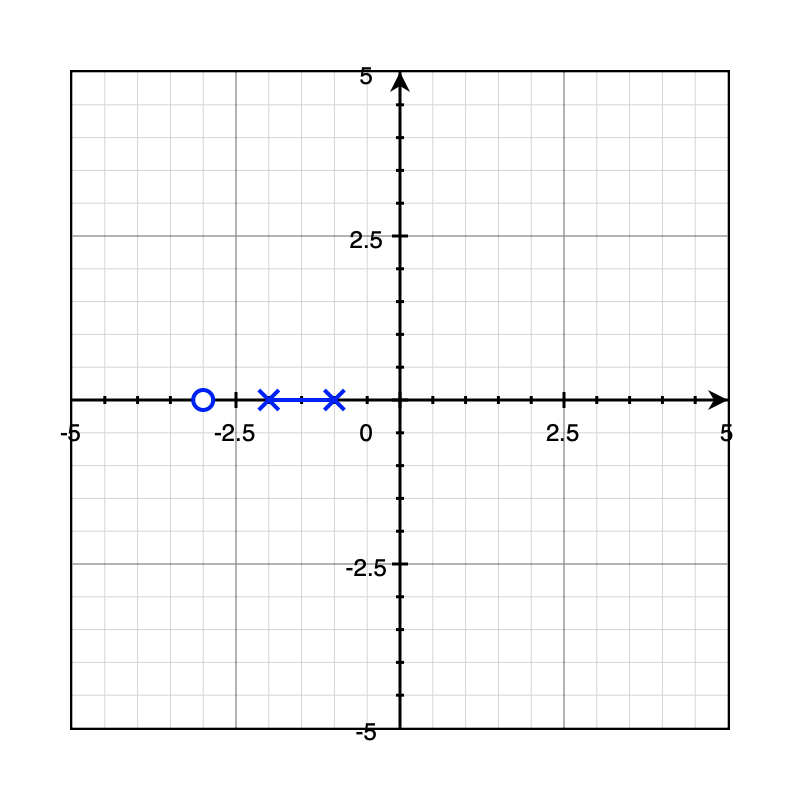
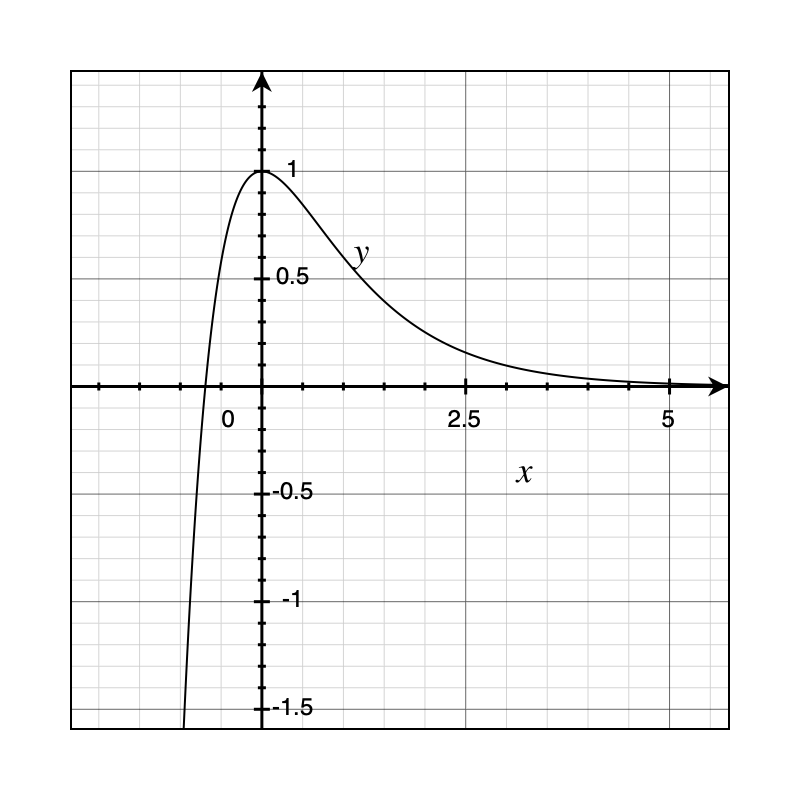
Example 4: Two poles and zero on the left \(\frac{s+3}{(s+2)(s+1)}\Rarr2e^{-t}-e^{-2t}\)

Example 5: Complex poles \(\frac{1}{(s+j\omega)(s-j\omega)}=\frac{1}{\omega}\frac{\omega^2}{(s^2+\omega^2)}\Rarr \frac 1 \omega \sin(\omega t)\) A pair of complex poles share the same real-components. In time-domain we have a sinusoidal signal. In this example, the pair of complex conjugate poles lie exactly on the imaginary axis. The result is a marginally stable system since the oscillation never goes away.

The same applies to if we add a zero-at-zero to to the transfer function: \(\frac{s}{(s+j\omega)(s-j\omega)}\Rarr \frac 1 \omega \cos(\omega t)\)

Example 6: Complex poles on the left \(\frac{1}{(s+a+j\omega)(s+a-j\omega)}=\frac{1}{\omega}\frac{\omega}{(s+a)^2+\omega^2}\Rarr\frac{1}{\omega}\sin(\omega t)e^{-at}\) If we shift the complex poles to the left hand side, then we essentially introduced a decaying exponential component to the system. This is due to the shifting theorem, that by shifting in the s-domain, we multiply the time-domain function by $e^{-at}$.

Example 7: Controlling an unstable system

Consider the following open loop transfer function: \(\frac{Y}{U}=\frac{2}{s-1}\Rarr 2e^t\) There exists a pole on the right hand side, so this system is unstable. To make it more stable, we need to add control/feedback. The simplest feedback we can add is this error feedback with a gain of 1.

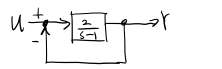
The closed loop transfer function is $G/(1+GH)$, where $G$ is the feedforward gain ($Y/U$) and $H$ is the feedback gain (1). The closed loop transfer function evaluates to: \(\frac{\frac{2}{s-1}}{1-\frac{2}{s-1}}=\frac{2}{s+1}\Rarr e^{-2t}\) Now this shows that the closed loop system is a stable system.