Week 4 - Electro-Mechanical Equivalences

There are mathematical similarities between linear electric systems and linear mechanical systems. Every electric system has resistance, capacitance, inductance, state of voltage, and current. Every mechanical system has mass, friction, spring, state of force, and velocity.

For the sake of consistency, let us define the following equivalence:

• Let current in an electrical system be equivalent \(\equiv\) to force in a mechanical system.

• Let voltage in an electrical system be equivalent \(\equiv\) to velocity in a mechanical system.

Note that we can define it the other way, but it means all of the equivalences for resistance, capacitance, inductors, etc will be flipped.

Ohm’s law is \(V=IZ\), and using our definitions, we can have an Ohm’s law for mechanical systems:

\[V=FZ\]

Where \(V\) is the velocity, \(F\) is the force, and \(Z\) is some mechanical impedance.

Electrical

Purely Resistive: in a purely resistive system, \(V=IR\) by Ohm’s law.

Purely Capacitive: in a purely capacitive system, \(V=I\frac{1}{sC}\) where \(\frac{1}{sC}\) is the impedance of the capacitor and \(s\) is the complex frequency \(j\omega\). Notice that we can rearrange the equation to:

\[V=\frac{1}{C}\frac{I}{s}\]

Recall from the Laplace transforms that division by \(s\) is integration \(\int\) in time domain. Thus the voltage in a purely capacitive system is a function of integration of current.

Purely Inductive: in a purely inductive system, \(V=IsL\), similarly, \(sL\) is the impedance of the inductor. However we can rearrange once again:

\[V=L(sI)\]

Recall multiplication by \(s\) is taking the derivative. Thus the voltage in a inductive system is a function of rate of change in current.

Mechanical

Purely Friction: in a system only consists of friction (such as a damper), \(F=BV\) where \(F\) is the force exerted, \(B\) is the friction coefficient, and \(V\) is velocity.

Since we defined earlier that \(V\) for velocity, then by rearranging we get the relationship

\[V=\frac{1}{B}F\]

The mechanical impedance for a system with only friction is \(Z=1/B\).

Purely Mass: in a system only consists of mass, \(F=ma\), where \(m\) is mass and \(a\) is acceleration. To relate this to \(V\), notice that \(a\) is first derivative of \(V\). In Laplace domain, this would simply be a multiplication by \(s\). Rearrange and we get:

\[V=\frac{1}{m}\frac{1}{s}F\]

Notice that we’re integrating force in time domain. The mechanical impedance is \(Z=1/ms\)

Purely Spring: in a spring system, the force by the spring is \(F=kx\) where \(x\) is the displacement. Note that we can relate \(V\) to \(x\) by integration, or division by \(s\) in Laplace domain. It follows:

\[V=\frac{1}k sF\]

Notice that we’re taking the derivative of force in time domain. The mechanical impedance is \(Z=s/k\).

Equivalence

By matching electrical and mechanical impedances, we get:

\[\boxed{ \begin{aligned} R &\equiv \frac{1}{B}\\ C &\equiv m \\ L&\equiv\frac{1}{k} \end{aligned} }\]

Thus, the following electrical LRC system driven by a current source is equivalent to a simple spring mass damper mechanical system driven by some force.

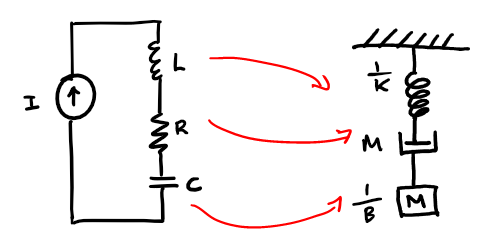
The two systems will have identical response:

• The current source will apply a constant current to the circuit / a uniform force applies to the spring-mass-damper system (i.e. gravity)
• The inductor will resist change in current / the spring will resist change in displacement
• The resistor will have a voltage drop that depends on the current / the damper will reduce speed that depends on force
• The capacitor will charge up and discharge / the mass will move and have momentum

Conversion

We can convert a mechanical system to electrical, or vise versa, and it makes it easy to solve the system (i.e. using mesh / nodal methods / MNA ¹ that works on circuits in spring-mass-damper systems).

Generally we can map the components in the two systems one-to-one, however there are some rules regarding the layout:

• No matter where a mass is in a mechanical system, one of its node in the electrical equivalence must be connected to ground
• If a force/velocity applied in a mechanical system is relative to ground, the equivalent current/voltage source in the electrical system must be connected to ground.

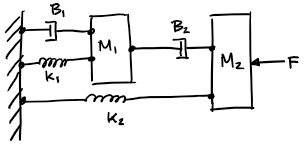
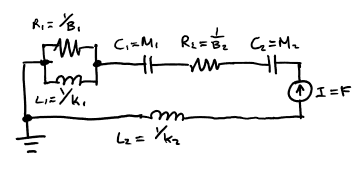
Example: convert the following mechanical system to its electrical equivalence

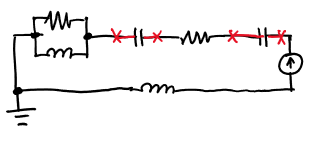
Naïve solution: We literally switch all the dampers with resisters, mass with capacitors, and springs with dampers. Then set the leftmost node connecting \(B_1\), \(k_1\) and \(k_2\) as ground.

This will not yield the same response as it’s not the same system. The two capacitors have none of its nodes connected ground.

Solution: Because we know that mass are relative to ground at all times, we start with capacitors, with one of its end nodes connected to reference.

insert

We also know that the applied force on \(M_2\) is relative to ground, so we add the current source to the node shared with \(M_2\), with the other end node connected to ground.

insert

Lastly, we can connect everything else.