W19 Assignment 2
Updated 2019-09-17
1. Comet Hale-Bopp
Comet Hale-Bopp has an orbital period of about 2450 years and an orbital eccentricity of of 0.995.
(a) What is the semi-major axis of Comet Hale-Bopp’s orbit?
We can apply Kepler’s third law: where the period of the planet’s orbit squared is directly proportional to the cube of the semi-major axis or the orbit.
In particular:
\[P_\text{yr}^2=a_\text{au}^3\]Then we can isolate and find the semi-major axis:
\[\begin{aligned} a_\text{au}&=\sqrt[3]{P_\text{yr}^2}\\ &=\sqrt[3]{2450^2}\\ &=181.7\text{au}\\ a&=\boxed{2.72\times 10^{10}\text{km}} \end{aligned}\]The semi-major axis of Hale-Bopp is 181.7 astronomical units or 2.72×1010 km, or 2.72×1013m.
(b) Use the orbital data of Comet Hale-Bopp to estimate the mass of the Sun.
Using derived Kepler’s third law, and assuming that the mass of the comet is much smaller than the mass of the Sun, we may proceed with the expression
\[P^2=\frac{4\pi^2}{GM}a^3\]We’re using the gravitational constant $G$ which has the units m3s-2kg-1. So we convert the previously calculated values and plug it into our equation.
\[\begin{aligned} M&=\frac{4\pi^2}{GP^2}a^3\\ &=\frac{4\pi^2}{\underbrace{6.67259\times10^{-11}}_{\frac{\text{m}^3}{\text{s}^2\text{kg}}}\underbrace{(2450\times365.25\times24\times60\times60)^2}_{\text{s}^2}}\underbrace{(2.72\times10^{10}\times10^3)^3}_{\text{m}^3}\\ &=\boxed{1.989\times10^{30}\text{kg}} \end{aligned}\]The mass of the sun is 1.989×1030 kg.
(c) Calculate the distance of Comet Hale-Bopp from the Sun at perihelion and at aphelion.
We start with the definition of an ellipse centered around one of the foci in polar coordinates:
\[r=\frac{a(1-e^2)}{1+e\cos\theta}\]At perihelion, $\cos\theta=1$, and at aphelion, $\cos\theta=0$. Then we simplify the equation, and let $r=q$ for $q$ being the distance at perihelion. Similarly, let $r=Q$ for $Q$ being the distance at aphelion. Thus:
\[q=a(1-e)\qquad Q=a(1+e)\]Plugging in the numbers:
\[\begin{aligned} q&=a(1-e)\\ &=(181.7)(1-0.995)\\ &=\boxed{0.909\text{au}}\\ Q&=a(1+e)\\ &=(181.7)(1+0.995)\\ &=\boxed{362.6\text{au}} \end{aligned}\]The perihelion and aphelion orbiting altitude of the comet around the sun is 0.909 au and 362.6 au respectively.
(d) Determine the orbital speed of the comet when at perihelion, at aphelion, and on the semi-minor axis of its orbit.
Using conservation of energy of an orbit’s kinetic and potential energy, we get the equation for speed in an elliptical orbit:
\[v^2=GM\left(\frac{2}{r}-\frac{1}{a}\right)\]Speed at perihelion ($r=q=0.909$ au):
\[v=\sqrt{GM_\odot\left(\frac{2}{0.909\times(1.496\times 10 ^{11})}\text{m}^{-1}-\frac{1}{2.72\times10 ^{13}}\text{m}^{-1}\right)}\\ v=\boxed{44,134\text{ m/s}}\]We perform the same calculation for speed at aphelion ($r=Q=362.6$ au):
\[v=\sqrt{GM_\odot\left(\frac{2}{362.6\times(1.496\times 10 ^{11})}\text{m}^{-1}-\frac{1}{2.72\times10 ^{13}}\text{m}^{-1}\right)}\\ v=\boxed{110.6\text{ m/s}}\]When the orbit is at the semi-minor axis, the orbit altitude equals to semi-minor axis $b$. Normally, we would need to calculate $ae$ and $b$ such that we can apply Pythagoreas theorem to find $r$, but because the orbit is so eccentric, we can approximate $r=a$ for when the comet is on the semi-minor axis.
The equation then simplfies down to
\[v=\sqrt{\frac{GM_\odot}{a}}\\ v=\boxed{2209\text{ m/s}}\]The orbiting speed for when the comit at perihelion, aphelion, and on the semi-minor axis is 44,134 m/s, 110.6 m/s, and 2209 m/s respectively.
(e) How many times larger is the kinetic energy of Comet Hale-Bopp at perihelion than at aphelion?
We need to find the ratio of kinetic energy:
\[\frac{E_{k_{pe}}}{E_{k_{ap}}}=\frac{0.5m v_{pe}^2}{0.5mv_{ap}^2}=\frac{v_{pe}^2}{v_{ap}^2}\]Which is just the ratio of the orbiting speed squared.
\[\frac{E_{k_{pe}}}{E_{k_{ap}}}=\frac{(4.41\times10^4 \text{m/s})^2}{(1.11\times10^2\text{m/s})^2}=\boxed{159,201}\]The kinetic energy for the comet is 1.59×105 times greater at perihelion than at aphelion.
2. Jupiter and Kepler’s 3rd Law
Verify that the general form of Kepler’s third law applies to the 4 Galilean moons of Jupiter (Io, Europa, Ganymede and Callisto).
(a) Using the data in Appendix C of the textbook, make graph of log10P vs. log10a. You may use graph paper or a plotting program.
Recall the general form of Kepler’s third law is given as:
\[P_\text{yr}^2=a_\text{au}^3\]Then the textbook Appendix C section gives us the data:
| Satellite | Orbital Period (days) | Semi-major axis (km) |
|---|---|---|
| Io | 1.769 | 421,600 |
| Europa | 3.551 | 670,900 |
| Ganymede | 7.155 | 1,070,400 |
| Callistro | 16.689 | 1882,,700 |
However, we need to also convert it into units that is appropriate to Kepler’s third law before we take the log10.
| Satellite | Orbital period (years) | Semi-major axis (au) | Log10P | Log10a |
|---|---|---|---|---|
| Io | 0.0048 | 0.0028 | -2.3149 | -2.5500 |
| Europa | 0.0097 | 0.0045 | -2.0122 | -2.3483 |
| Ganymede | 0.0196 | 0.0072 | -1.7080 | -2.1454 |
| Callistro | 0.0457 | 0.0126 | -1.3402 | -1.9001 |
Then we plot the log’d values (last two columns):
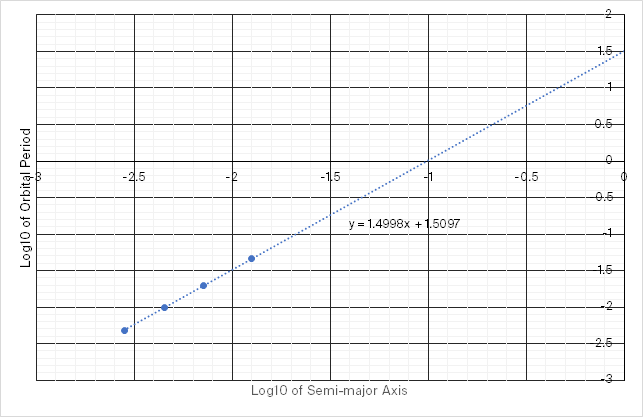
(b) Show that the slope of a straight line through the data is 3/2.
The slope of a linear line of best fit for the graph from part A is 1.4998, which is close enough to 3/2.
(c) Calculate the mass of Jupiter from the value of the y-intercept of your graph.
The y-intercept of the graph is at $y=0$, $x=-1$. AKA, $\log {10}P=0$, and $\log{10}a=-1$. Then we “un-log” the two values by raising them to the 10 to the power of. We get:
\[P=10^0=1\text{yr}\\ a=10^{-1}=0.1\text{au}\]Now we can proceed with isolating $M_\text{jup}$ from the equation relating period to semi-major axis:
\[\begin{aligned} P^2&=\frac{4\pi^2}{GM_\text{jup}}a^3\\ M_\text{jup}&=\frac{4\pi^2}{GP^2}a^3\\ &=\frac{4\pi^2}{G\underbrace{(365.25\times24\times60\times60)^2}_{\text{s}^2}}\underbrace{(1.496\times10^{10})^3}_{\text{m}^3}\\ &=\boxed{1.989\times10^{27}\text{kg}} \end{aligned}\]The mass of Jupiter is 1.989×1027 kg.
3. Orbits and More Approximations
(a) Consider a satellite in a circular, low-Earth orbit, where the satellite’s elevation h about the Earth’s surface is $h\ll R_\oplus$. Show that the orbital period $P$ for such a satellite is approximately $R=C(1+3h/2R_\oplus)$. What is the numerical constant $C$ in minutes?
Let’s start with the period of a circular orbit. The speed of a given circular orbit is:
\[v_c=\sqrt{\frac{GM_\oplus}{R_\oplus+h}}\]And assume that the circumference / total arc length of a full revolution is:
\[2\pi(R_\oplus+h)\]Period is given by:
\[time=distance/speed\\ P=\frac{2\pi(R_\oplus+h)}{\sqrt{\frac{GM_\oplus}{R_\oplus+h}}}\]Simplifying a bit, and I’m assigning the variable $\zeta$ to the constant part:
\[\begin{aligned} P&=\underbrace{\frac{2\pi}{\sqrt{GM_\oplus}}}_\zeta(R_\oplus+h)\sqrt{R_\oplus+h}\\ &=\zeta R_\oplus\left(1+\frac{h}{R_\oplus}\right)\sqrt{R_\oplus}\left(\sqrt{1+\frac{h}{R_\oplus}}\right)\\ &=\zeta R_\oplus^{3/2}\left(1+\frac{h}{R_\oplus}\right)^{3/2} \end{aligned}\]We can see that there is a binomial series, so we can approximate the value using Taylor expansion for binomial series. Suppose $x=h/R_\oplus$, and let $\alpha=3/2$, then the expansion is:
\[(1+x)^\alpha=\sum_{n=0}{\alpha \choose n}x^n=1+\alpha x+\frac{\alpha(\alpha-1)}{2!}x^2+\dots\]We can just approximate by truncating everything after the linear term ($\alpha x$). So:
\[\begin{aligned} (1+x)^\alpha&=1+\alpha x\\ \left(1+\frac{h}{R_\oplus}\right)^{\frac{3}{2}}&=1+\frac{3}{2}\frac{h}{R_\oplus} \end{aligned}\]Now plugging everything back:
\[\begin{aligned} P&=\zeta R_\oplus^{\frac{3}{2}}\left(1+\frac{3h}{2R_\oplus}\right)\\ &=\underbrace{\left(\frac{2\pi R_\oplus^{\frac{3}{2}}}{\sqrt{GM_\oplus}}\right)}_C\left(1+\frac{3h}{2R_\oplus}\right) \end{aligned}\]Computing for $C$, we get 5070 seconds or 84.5 minutes.
(b) What is the orbital period for a low-lunar orbit, as was used by the Apollo command modules?
According to Wikipedia 1, the low lunar orbit is about 100km above the moon’s surface. And they have a orbital period of about 2 hours.
-
Lunar Orbit: https://en.wikipedia.org/wiki/Lunar_orbit ↩