Solar System Energy

Planetary energy balance:

Blackbody Emission

AKA blackbody radiation.

There are two conditions required for blackbody radiation:

1. The body must be in thermal equilibrium - has a well-defined temperature T

2. The body is dense/opaque such that photos can’t simply pass through it but instead bounce around many times on the way to exiting.

The total flux of blackbody radiation is given by: \(F=\sigma T^4\quad[\text{Js}^{-1}\text{m}^{-2}]\) Where $\sigma$ is the Stefan-Boltzmann constant which is 5.56×10^-8 Js^-1m^-2K^-4.

For humans, our body is at 310 K, objects radiate about 500Wm^-2 where 1W is 1Js^-1. If the average human surface area is 2m² then we radiate about 1000W.

The surface of the Sun is around 5780K. Which radiates about 6.3×10⁶ Wm^-2.

Now we looked at the total flux, it’s actually an integral of the intensity for all wavelengths: \(F=\sigma T^4 = \pi\int_0^\infty I_\lambda \mathrm d\lambda\) Where $I_\lambda$ is the intensity per unit wavelength.

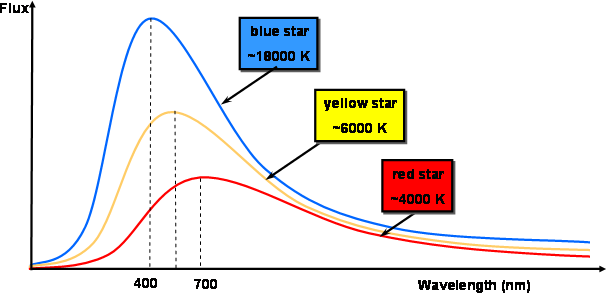
Temperature is the only parameter needed to describe the blackbody radiation.