Celestial Mechanics

Kepler’s Three Laws

Kepler’s three laws are descriptions based on physical observations and can be used to predict.

Law 1: Law of Ellipses

Planets travel on elliptical orbits around the sun, where the sun is located at one focus of the ellipse.

Law 2: Law of Equal Areas

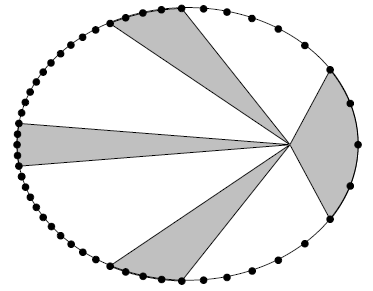
A line connecting a planet to the sun sweeps out equal area in equal time interval, regardless of planet’s position. Thus the second law also implies that planet’s orbital speed depends on its location.

Law 3: The Harmonic Law

The harmonic law is given by: $P^2=a^3$ Where $P$ is the orbit period of the planet in years, and $a$ is the average distance / average orbital altitude of the planet from the sun measured in astronomical unit (AU).

Ellipses

Properties of an Eclipse

In cartesian, the ellipse is given by: $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ An eclipse is also defined by a set of points that satisfies the equation $r+r'=2a$

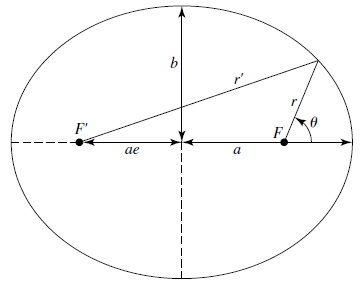
• $a$ is the semimajor axis (long axis).
• $b$ is the semi-minor axis (short axis).
• $e$ (0≤ $e$ ≤ 1) is the eccentricity, the fractional distance of the foci to the geometric center.
• $r$ and $r’$ are the distances from the two foci to a point on the ellipse. $r+r’$ is always constant (definition of an ellipse).
• $F$ and $F’$ are the two foci, $F$ being the principal focus.
• Perihelion is the point on the ellipse closes to the principal focus.
• Aphelion is the point on the ellipse farthest from the principal focus.

If $r=r’$, then using Pythagorean theorem, we can derive: $b^2=a^2(1-e^2)$

Area

The area of the ellipse is: $A=\pi ab = \pi a^2 e$

Polar Definition

The polar equation of ellipse centered around one of the focus given by: $r=\frac{a(1-e^2)}{1+e\cos\theta}\quad (0\leq e \lt 1)$ When $e$ is in between 0 and 1, we use the above definition as it makes an ellipse. But an ellipse is one of the conic sections. For different ranges of $e$, we may get a parabola or hyperbola. $\begin{cases} \text{if }e =0:& r=a\quad\text{(circle)}\\ \text{if }0\leq e \lt 1:&r=\frac{a(1-e^2)}{1+e\cos\theta} \quad\text{(ellipse)}\\ \text{if }e =1:&r=\frac{a}{1+\cos\theta}\quad\text{(parabola)}\\ \text{if }e \gt 1:& r=\frac{a(e^2-1)}{1+e\cos\theta}\quad\text{(hyperbola)} \end{cases}$

Elliptical Motion

The elliptical motion of planets follow Newton’s law of motion and gravity.

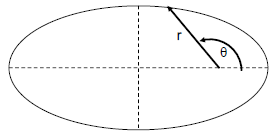
Recall the ellipse in polar coordinates centered around one focus is $r=\frac{a(1-e^2)}{1+e\cos\theta}$

This describes the following ellipse:

• When $\theta=0$, the planet is at its perihelion. The orbiting “altitude” $q$ is:

  $$q=\frac{a(1-e^2)}{1+e}=\frac{a(1-e)(1+e)}{1+e}=\boxed{a(1-e)}$$

• When $\theta=\pi$, the planet is at is aphelion. The orbiting altitude $Q$ is:

  $$Q=\frac{a(1-e)(1+e)}{1-e}=\boxed{a(1+e)}$$

Slanted Ellipses

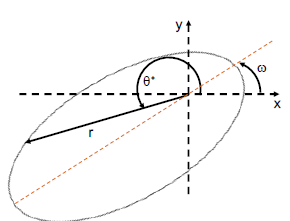
The ellipse may be slanted from our point of reference (x-y grid). The slant is described by longitutde of perihelion or $\omega$. The angle $\theta^\star$ is still in reference to the x-axis. The modified polar equation becomes: $r=\frac{a(1-e^2)}{1+e\cos(\theta^\star-\omega)}$

Velocity & Radius

The velocity and radius are inversely proportional due to conservation of angular momentum.

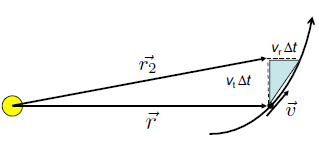
Let the area $A$ be the area of the large white triangle. The change in area is $\Delta A=\frac{1}{2}(v_t\Delta t)(r)$

Example: Kepler’s 2nd law using calculus

insert slide diagram

Start at $\vec r$ and go a short timestep $\Delta t$ into the future. Then as $\Delta t\rarr 0$ ,the area of the blue triangle approaches 0. The blue triangle area is given by the vertical and horizontal position differences: $v_t\Delta t\times v_r \Delta t \over 2$.

The area of the main triangle is basically: $dA=\frac{1}{2}(v_t\Delta t)(r)$ As $\Delta t$ approaches 0, then we have $\frac{dA}{dt}=\frac12 r v_t=\frac{1}{2}rv$ which equals some constant (that’s Kepler’s 2nd law).

Therefore $v$ is proportional to the inverse of the orbit altitude ($\frac{1}{r}$). AKA the planet speeds up at perihelion.

Notice the relationship of $rv=C$ where $C$ is a constant is the conservation of angular momentum. Therefore the angular momentum is constant.

insert diagram in polar

Example: in polar

The arclength $s$ is just $s=r\theta$ for $\theta$ in radians. Then the velocity $v_t=r\dot{\theta}$, where $\dot\theta=\frac{\mathrm d\theta}{\mathrm d t}$.

$r^2\dot \theta = \frac L M $ is a conserved quantity. This is from $\frac{\mathrm dA}{\mathrm dt}=\frac12 (r)(r\dot\theta)$.

Finding an expression for $\theta$?

Kepler figured it out (Kepler’s method):

insert slide 19

1. Draw a circle circumscribing the ellipse such that $r_{circ}=a$. Where $a$ is ellipse’s semimajor axis.
2. Position $r$ and $\theta$ for point $P$ on planet’s orbit, drop a perpendicular line from the point to the semimajor axis. Extend that line upward to meet the outer circle, make that intersection point $D$.
3. The angle between the x-axis and the line from geometric center to $D$ is the angle $E$, or “eccentric anomaly/angle”.

It turns out we can write: $r=a(1-e\cos(E))$

where $e$ is eccentricity. We get this from $r_x=ae-a\cos E$ and $r_y=b \sin E$ (using small dashed circle).

We also find that: $\tan\left(\frac{\theta}{2}\right)=\sqrt{\frac{1+e}{1-e}}\tan(E/2)$

1. As a function of time $t^$ since perihelion, we get Kepler’s equation (this equation is a transcendental equation, which cannot be solved analytically): $E-e\sin E =nt^*$ And mean motion is the average advance in radians per unit of time: $n=\frac{2\pi}{P}$ And $nt^$ is the mean anomaly which is a fictitious angle that advances uniformly in time.