Astronomy Basics
Updated 2019-09-06
Angles
In a full revolution there are 360 degrees. For each 1 degrees, there is 60 arc minutes, and for each arc minute, there is 60 arc seconds. Therefore, there are 3600 arcseconds in 1 degrees, or 1,296,000 arcseconds in a full revolution.
Solid Angles
Solid angle is an “angular area” specified by 2 dimensions that describe an area that occupies a spherical view. Suppose we’re standing inside a sphere with radius $r$, and looking at an area $A$ on the surface of the sphere, then the solid angle $\Omega$ occupied by $A$ will be $A\over r^2$. Note that $r$ is not to be confused with radius of the circle of area $A$. \(\Omega=\frac{A}{r^2}\)
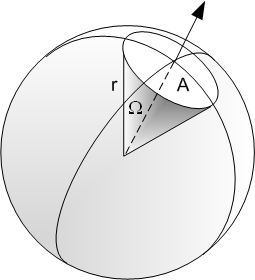
The unit for solid angles is steradians. It is also possible to specify solid angles with square degrees, square arcminutes, and square arcseconds.
Given that the surface area of a sphere is $4\pi r^2$, then the solid angle that covers the entire sphere is therefore $4\pi$.
Small Angle Approximation
If a given angle θ is very small, then there is very little practical difference between the opposite edge length of the angle versus the opposite arclength.
\[\theta={c \over r}\approx \arctan\left({d\over l}\right)\]Angular Diameter
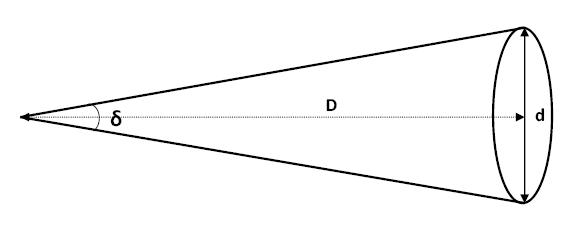
Angular diameter $\delta$ is the one-dimensional angle that covers a specific diameter $d$ with $D$ distance away.
\[\delta_\text{rad}=\frac{d}{D}\]What is the angular diameter of an object 1,000km across, 10,000,000 km away?
In radians: \(\delta=\frac{d}{D}=0.0001\) In arcseconds: \(\delta = 0.0001\times\left(\frac{180\deg}{\pi}\right)\left(\frac{3600"}{1\deg}\right)=20.6"\) To calculate solid angle, recall that the solid angle is given by the area of the object seen divided by the distance to the object squared.
\[\Omega=\frac A {D^2}=\frac{\pi\left(\frac{1000\text{km}}{2}\right)^2}{(1\times10^7)^2}=7.85\times10^{-9}\text{sr}\]We obtain 7.85×10-9 steradians (sr). Because solid angle is a two-dimensional unit, when we convert between steradians to square degrees or square arcseconds, etc. we need to square all the conversion factors.
The solid angle in square arcseconds is given by:
\[\Omega_{\text{arcsec}^2}=\Omega\times\left(\frac{360\text{deg}}{2\pi}\right)^2\times(60\text{'/deg}\times60\text{"/'})^2\]Using this conversion, we get 334 square arcseconds.