Muchen He :: 44638154
Midterm 1
Q1. Engineering Economics considers the economic aspects of decision making. What criteria other than economics factor into engineering decision making for large, complex projects (name two)?
In larger, complex projects we also need to consider:
Environmental impacts
- How does the project affect nearly resource, wildlife, carbon footprint, actual land footprint, noise produced, pollution produced
Social impacts:
- How does the project influence/influenced by the externalities
- How does the project affect jobs markets, reputation, population consensus, residences
Q2. What does marginal revenue represent? What are sunk costs?
Marginal revenue is the revenue gained from producing one more unit. The sunk costs are costs that’s already spent and is not recoverable. The sunk costs should not affect future economic decisions.
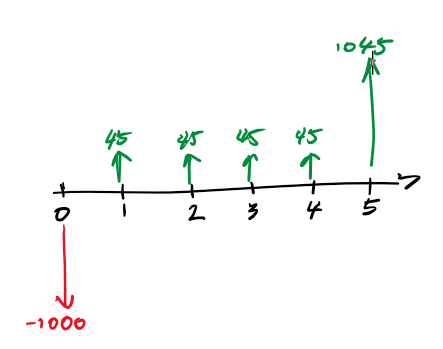
Q3. Create a cash flow diagram for an investment in a savings bond. The bond costs $1,000, pays $45 in interest per year for five years, and pays back the principle in its entirety at the end of the five years.
Q4. You are planning on purchasing a house and will take out a mortgage for $200,000 to do so. The bank charges 3.6% interest compounded semi-annually, and you will be making monthly payments. If you pay back the loan over 25 years, what will be your monthly payment amount?
The present value is $200,000. The compounding period and payment period is different so we want to the find the equivalent interest for period, where is number of compound periods per year, and is the number of payments per year:
The total number of payment periods will be . Then use capital recovery factor on the present value of $200,000. We get as monthly payment.
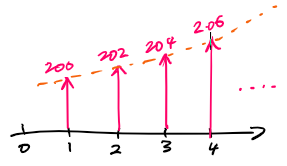
Q5. You wish to donate to an endowment fund to establish a scholarship. You want the scholarship to pay $5000 every year. Being somewhat quirky, you also want the fund to pay out a $10,000 scholarship (in addition to the $5000) every leap year. If the endowment fund earns an annual return of 8%, how much do you need to donate to provide for this set of scholarships forever? (assume a leap year occurs every four years. Assume the first leap year will be in the fourth year after the scholarship is established).
This becomes a perpetuity, we can split this problem into two independent parts:
- We receive $5,000 every year, how much do we donate?
- We receive $10,000 every four years, how much do we donate?
For the first part:
For the second part, we need to find the equivalent annual cashflow. So taking the cashflow of $10,000 every four years, at a rate of 8% each year, we get a present worth of $27,740, the equivalent annual cash flow would be $2,228.
So we need to invest a total of
Q6. The modified internal rate of return (MIRR) requires two external rates to determine the internal rate of return. What do the two external rates represent?
The two external rates are usually the loan rate - the the money that we borrowed, and the investment rate - for the money that we used to invest.
Q7. Two projects have the following cashflows. If you have a payback period of two years, which project should you choose? Why might this be a poor decision?
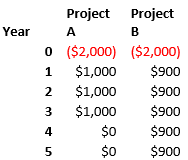
Given that the payback period is two years, neither would be a good decision as we will be operating at a loss. Nonetheless if we had to choose, we should choose to do nothing.
If ‘nothing’ is not an available option, then go with project A as it will yield more immediate income in year 1 and 2. However, because money is worth more now than future, project A would still be at a loss.
Q8. Economies of scale suggests that generally, as you produce more of something, the average cost of production will go down. However, in some cases producing more output results in increased average costs. Give an example of why this might happen for a factory producing widgets.
Generally the average cost will go down because:
- There is a fixed cost
- Marginal cost decreases (economies of scale, learning curve, etc.)
The average cost of producing widgets might go up if we have to expand the facility (increasing fixed costs), hiring new people, or too much automation like Elon Musk’s case (decreased productivity).
Q9. For the following Profit and Loss chart:
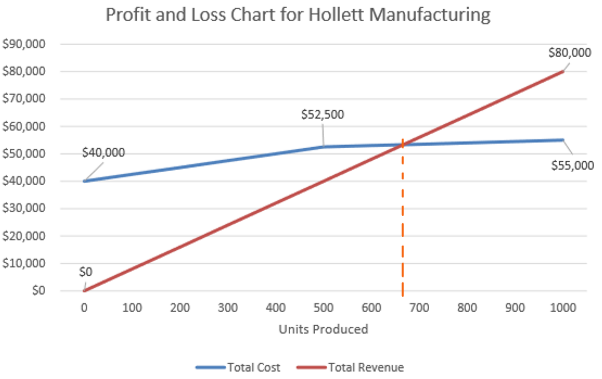
What is the break even point in terms of units produced?
Breakeven point is when total cost total revenue. This is the intersection that occurred at around 660th unit.
What are the fixed costs for the facility?
This is the cost when no units are produced, which is $40,000.
What are the variable costs for producing the product?
The variable cost is the incremental cost for producing one more unit, which is or the slope. The variable cost for producing less than 500 units is
The variable cost for units after 500th units is
What is the marginal revenue for this product?
The marginal revenue is the revenue for producing one more unit. Since the relationship between the revenue is linear and doesn’t change. The marginal revenue is the slope:
What is the average cost of production for the full 1000 units? What is the average cost of production at 500 units?
For 1000 units, the total cost is $55,000. The average cost is
For 500 units, the total cost is $52500. Thus the average cost now is
Q10. You want to save $75,000 to purchase start a small pizza franchise. You intend to start saving $200 per month, and increase your monthly savings by 1% per month.
You will save the money in a high interest savings account that pays 3% interest per year, compounded monthly. After fifteen years, will you have sufficient money saved?
First, the monthly interest rate monthly is simply . Our payment cashflow is a geometric gradient series with growth rate .
The interest rate is not the same as the growth rate . The future value is given as follows. Where the first payment is $200. And number of periods is .
Converting the future value back to present value gives:
So yes, we will have sufficient money.
Q11. You are evaluating replacing a conveyor belt that moves wood chips at a pulp mill.
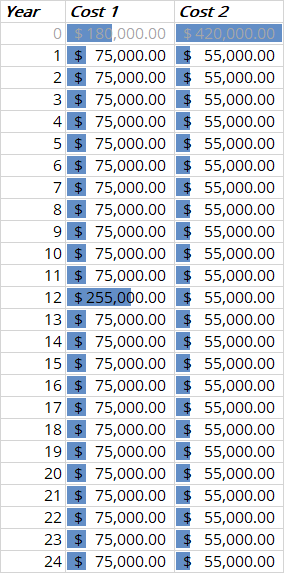
Option 1 is a rubber belt conveyor. It will cost $180,000 up front and have annual operational and maintenance costs of $75,000. This conveyor will last 12 years.
Option 2 is a chain conveyor. It will cost $420,000 to install and have annual costs of $55,000. It will last 24 years.
Evaluate the two alternatives and recommend the cheaper option using Equivalent Annual Cashflow analysis. The interest rate for the pulp mill is 12%
Since the two alternatives has lifetime LCM of a nice 24 years, we will use that as our analysis period. We also assume repeatable purchases so option 1 has to be purchased twice in total.
First we will model the cashflow for 24 years for both alternatives. Since option 1 only has 12 years of useful life, we need to purchase another one for and additional $180,000 on year 12.
This enables us to find the present value of costs for both options (using the
NPVfunction).
Then we can find the equivalent annual cash flow or annuity given the present value of costs using the
PMTfunction.
Since option 1 has lower equivalent uniform annual costs, we should go with option 1.
Q12. You purchase some shares in an energy company. You hold the shares for many years, and in many, but not all, years collect dividends and collect dividends every year starting with the first. Getting ready for retirement, you sell the shares. You purchase the shares for $10,000, and sell them after 15 years for $18,000. Every year, the shares pay you $400 in dividends. Calculate the rate of return you received on this investment.
If you use the guess and iterate method, only do calculations for your first guess, and indicate what your second guess would be. If you use a spreadsheet to calculate the IRR, also demonstrate your answer is correct by showing the NPV of the investment at your calculated IRR. Show the table of values and the functions you used so the marker can replicate the results.
The net present value (NPV) can be written as follows as a function of , the IRR we want to solve for:
For IRR, we need NPV to equate to 0. We can try 0% for first:
For the reset of the values, Excel is used to automate computations.
The NPV formula used in Excel is as follows. Note that negative sign is used in the
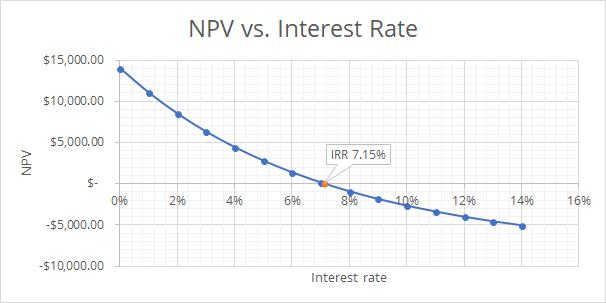
PVfunction because the function works on costs but the $400 dividends and $18,000 salvage value are income. Also note thatE22in the equation is the interest rate.=-10000+PV(E22,15,400)+PV(E22,15,0,-18000)We can plot NPV vs. graph:
Finally, the internal rate of return is 7.15%.
The full spreadsheet for this question can be accessed here.
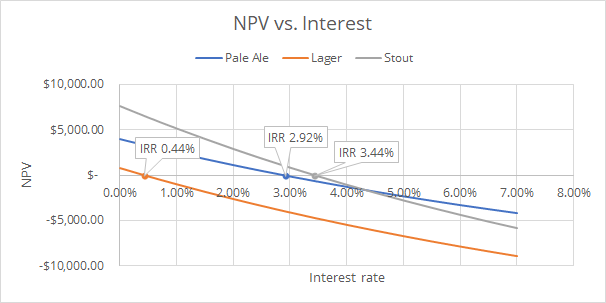
Q13. You have started a small brewery and are deciding what batch to brew next. You are considering three options, but only have the facilities to do one. You have estimated to costs to prepare each of the batches, and your chief of marketing has given you the expected sales for each. A batch of any beer will brew sufficient volume to support sales for 12 months.
| Pale Ale | Lager | Stout | |
|---|---|---|---|
| Initial cost | $20,000 | $28,000 | $32,000 |
| Monthly sales | $2000 | $2400 | $3300 |
Using incremental analysis, which beer should you brew? You have a minimum acceptable rate of return of 30% per year.
Let the analysis period be 1 year (12 months) and let the subperiod be 1 month. The general NPV can be formulated as:
Where is the monthly interest rate and is the initial cost. Now we can compute the present worth for all options using MARR. Note the monthly MARR, then is . We plot the three alternatives’ NPV vs. graph using the same method outlined in question 12:
Note that the Lager alternative has internal rate of return of only 0.44%, below the monthly MARR of 2.5%. Thus we eliminate it from the upcoming incremental analysis.
Let’s perform incremental analysis on increment StoutPale Ale:
The initial cost of stout minus the initial cost of pale ale is , and the different of monthly benefit is . We find the incremental rate of return by equating cost and benefits:
The IRR of increment StoutPale Ale analysis is 4.29%. It is above the monthly MARR of 2.5%. Therefore brewing and selling stout is preferred.
The full spreadsheet for this question can be accessed here*.