Last updated 2018-07-25 by Muchen He (44638154)

Assignment 3Problem 1DescriptionAnalysisSimulationMinimum and MaximumProblem 2DescriptionAnalysisBonus

Assignment 3

Problem 1

Description

Through a series of strange and unlikely events, you find yourself in the lucrative business of cocaine smuggling. A new lab in your organization has recently started production, and you are responsible for distributing it.

The lab will produce 5000 kg of cocaine per year, at a cost of $2000 per kg. You are looking at shipping the cocaine to Miami by smuggling it in shipping containers through the port. You can smuggle 1000 kg of cocaine in a single shipment in this manner. Your cost of shipping is $500 per kg.

Based on historical records, you estimate each shipment has between a 5% and 15% chance of being caught and confiscated. If a shipment is not confiscated, it will be sold to your network of dealers in the area. Sales prices have typically had an average of $14,000 per kg, with a standard deviation of $3,000 per kg.

Use a simulation to estimate your expected profits for running this operation for one year. Also evaluate the risks by looking at other characteristics, such as the likelihood of losing money, maximum and minimum expected profits, and other such factors.

Analysis

We have a yearly production of 5000kg and can ship 1000kg at once. So there are five shipments a year.

The total variable cost of production and shipping for each shipment is

$(\$2000+\$500)[\text{/kg}]\times 1000[\text{kg}]=\$2.5\mathrm M$

If the shipment is caught, then the revenue for that shipment is $0. Otherwise, it is a realization of a random variable which follows the normal distribution with $\mu=14000$ and $\sigma=3000$ .

Theoretically, this is what we expect to happen:

Since the chance of being caught is 5-15% uniformly distributed, the expected value is simply

$\frac{0.05+0.15}{2}=10\%$

When the shipment is not caught, the expected value of the revenue is simply $\mu=\$14000[\text{/kg}]$ . Thus we have two case with probabilities, where $x$ is profit and the $2500 deficit per kg is the total cost for one kg in one shipment:

$\mathbb P(x)= \begin{cases} 0.9,&x=14000-2500\\ 0.1,&x=-2500 \end{cases}$

The final expected value of profit is:

$\mathbb E[\text{Profit}]=(11500)(0.9)+(0.1)(-2500)=\$10,100[\text{/kg}]$

The variance and standard deviation of the profit is

$\begin{aligned} \sigma^2&=\mathbb E[X^2]-\mathbb E[X]^2\\ &=\sum_x x^2\mathbb P(x)-\left(\sum_x x\mathbb P(x)\right)^2\\ &=[(11,500^2)(0.9)+(-2500)^2(0.1)]-(10,100)^2\\ &=\$17,640,000\\ \sigma&=\$4,200 \end{aligned}$

Simulation

The simulation is ran in R, here is the code:


xxxxxxxxxx
# Simulation constants
ITERATIONS <- 50000
# Problem constants
SHIPMENT_PER_YEAR <- 5   # [ul]
KG_PER_SHIPMENT <- 1000  # [kg]
PROD_COST <- 2000        # [$/kg]
SHIPPING_COST <- 500     # [$/kg]
CONFISCATE_LOW <- 0.05   # [ul]
CONFISCATE_HIGH <- 0.15  # [ul]
SALE_AVG <- 14000        # [$/kg]
SALE_STD <- 3000         # [$/kg]
# Performs a single shipment, returns nothing if shipment is confiscated
shipDrugs = function() {
    if (runif(1, 0, 1) < runif(1, CONFISCATE_LOW, CONFISCATE_HIGH)) {
        # Confiscated
        return(0) # [$]
    } else {
        # Generate revenue based on normal distribution and get total revenue
        return(rnorm(1, SALE_AVG, SALE_STD) * KG_PER_SHIPMENT) # [$]
    }
}
# Simulate
g_profits <- c()
simulate = function() {
    failedShipment <- 0
    profits <- c()
    for (i in 1:ITERATIONS) {
        # Cost
        yearlyCost <- SHIPMENT_PER_YEAR * KG_PER_SHIPMENT * (PROD_COST + SHIPPING_COST) # [$]
        
        # Benefits
        yearlyRevenue <- 0 # [$]
        for (n in 1:SHIPMENT_PER_YEAR) {
            revenue <- shipDrugs()
            if (revenue == 0) {
                failedShipment <- failedShipment + 1
            }
            # Add to yearly
            yearlyRevenue <- yearlyRevenue + shipDrugs() # [$]
        }
        
        # Profit
        profits <- append(profits, yearlyRevenue - yearlyCost)
    }
    
    # Result
    profitAvg <- mean(profits) # [$/year]
    profitSd <- sd(profits)    # [$/year]
    cat("Average profit: ")
    print(profitAvg)
    
    cat("Profit standard deviation: ")
    print(profitSd)
    cat("Overall caught probability: ")
    print(failedShipment / ITERATIONS / SHIPMENT_PER_YEAR)
    
    cat("Probability of losing money in a year: ")
    print(length(which(profits <= 0)) / length(profits))
    
    cat("Expected min ")
    print(profitAvg - 3*profitSd)
    
    cat("Expected max: ")
    print(profitAvg + 3*profitSd)
    # diagram
    hist(profits)
}
# Simulate
simulate()

The simulation ran for 10000 iterations, each iteration represents a year. The output of the simulation is the average profit each year, and the standard deviation of profits per year.


xxxxxxxxxx
Average profit: [1] 50487797
Profit standard deviation: [1] 11287709
Overall caught probability: [1] 0.1005
Probability of losing money in a year: [1] 0.00016

Which reads $50,487,797 in profit per year. Or average of $10,098 per kg. The standard deviation is $11,287,709 per year, or $2257.54 per kg. This is very close to our calculated result.

The overall probability of having a shipment caught is 10%. So there is a 10% chance that the shipment will be a loss.

Out of 10000 iterations/years, on average 1.6 iterations/years are operating at a loss. This translates to 0.016% chance of negative profit in one year of operation.

A histogram of all iterations/years in the simulation is show as below:

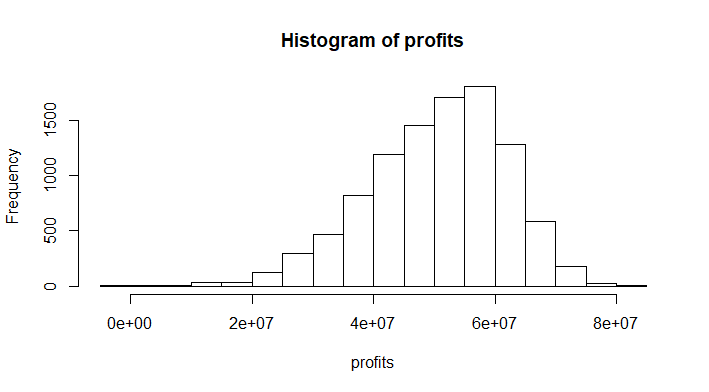
1532488890138

Notice that the shape is loosely resembling a normal distribution curve, except it’s asymmetrical and tends towards the lower side. This is due to the 5-15% chance of being caught.

Also notice that even though the chance is small, there are occurrences where we make zero to negative profits.

Minimum and Maximum

We shall look at the minimum and maximum profit by using the general rule where the minimum is $\mu-3\sigma$ (the bottom 0.2 percentile) and maximum is $\mu+3\sigma$ (the top 99.7 percentile). Where $\mu$ , the average profit, established in the previous section is $10,098/kg or $50.5M a year. The standard deviation, $\sigma$ , is $11.29M a year.

The minimum expected profit is then $16.63M, or $3,326/kg, and the maximum expected profit is $84.37M, or $16.874k/kg.

Problem 2

Description

You are considering purchasing a small aircraft as an alternate means of smuggling the cocaine. The aircraft would cost $2,000,000 and should last for five years, with no resale value (you can guess why).

There are two potential scenarios for cocaine demand – low demand, which would result in a net benefit of $2,000,000 per year for the next five years. Or high demand, which would result in a net benefit of $3,000,000 per year for the next five years. You estimate the likelihood is about 60% for low demand and 40% for high.

There is a chance the aircraft will be caught and confiscated by the border authorities. You estimate there is a 20% chance of this happening, in which case you would only get one year of benefits from the aircraft. You estimate the odds of the aircraft not being confiscated at 80%, for which you would get a full five years of benefits.

What is your expected IRR for purchasing this aircraft, and using the rule of thumb about acceptable risk levels, would you recommend moving ahead with it?

Analysis

The spreadsheet scrap work for this problem is available here.

There are four possible outcomes. First it is randomly determined that there will be high or low demand. Then it will be determined if the plane gets confiscated or not. Here is a table of the possible outcome and their associate joint probabilities:

	High demand (40%)	Low demand (60%)
Confiscated (20%)	Case A: (20%)(40%)=8%	Case B: (20%)(60%)=12%
Not confiscated (80%)	Case C: (80%)(40%)=32%	Case D: (80%)(60%)=48%

We can then plot the cashflow for all four cases for five years:

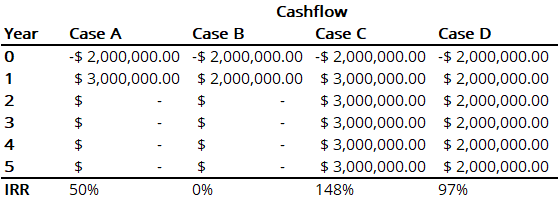
1532532110332

The internal rate of return is computed using the =IRR(...) function. From now, we can compute the statistical values.

The expected value of IRR is

$\begin{aligned} \mathbb E[\text{IRR}]&=\sum_i \text{IRR}_i\mathbb P_i\\ &=(0.5)(0.08)+0+(1.48)(0.32)+(0.97)(0.48)\\ &=0.979 \end{aligned}$

The variance of the IRR is

$\begin{aligned} \sigma^2&=\mathbb E[\text{IRR}^2-\mathbb E[\text{IRR}]^2]\\ &=[(0.5)^2(0.08)+0+(1.48)^2(0.32)+(0.97)^2(0.48)]-(0.979)^2\\ &=0.215 \end{aligned}$

Take the square root of the variance reveals the standard deviation:

$\sigma=\sqrt{0.215}=0.464$

The rule of thumb expresses that economic decision should be taken if the risk to rate of return ratio is low, such as a 2:1 ratio. In this case, $\frac{\text{IRR}}{\sigma}=\frac{0.979}{0.464}\gt 2$ . Therefore it would be wise to buy the aircraft to transport drugs.

Furthermore, in this particular scenario, we actually don’t need to use the general rule of thumb because the worst case, the case where there is low demand and plane confiscated would return zero loss. There is literally nothing to lose.

narcos-plane

Bonus

The cartel operated under Pablo Escobar is the Medellín Cartel. (Source: Wikipedia, but actually Netflix 😂)